368091 In young's double slit experiment, the two slits are '\(d\)' distance apart. Interference pattern is observed on the screen at a distance '\(D\)' from the slits. First dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
368093
In a Young's double slit experiment, two slits are illuminated with a light of wavelength 800 nm . The line joining \(A_{1} P\) is perpendicular to \(A_{1} A_{2}\) as shown in the figure.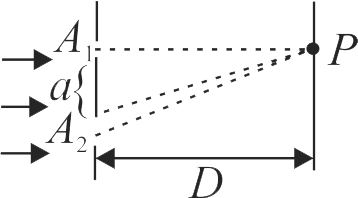
If the first minimum is detected at \(P\), the value of slits separation '\(a\)' will be the distance of screen from slits \(D = 5\,cm.\)
368091 In young's double slit experiment, the two slits are '\(d\)' distance apart. Interference pattern is observed on the screen at a distance '\(D\)' from the slits. First dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
368093
In a Young's double slit experiment, two slits are illuminated with a light of wavelength 800 nm . The line joining \(A_{1} P\) is perpendicular to \(A_{1} A_{2}\) as shown in the figure.
If the first minimum is detected at \(P\), the value of slits separation '\(a\)' will be the distance of screen from slits \(D = 5\,cm.\)
368091 In young's double slit experiment, the two slits are '\(d\)' distance apart. Interference pattern is observed on the screen at a distance '\(D\)' from the slits. First dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
368093
In a Young's double slit experiment, two slits are illuminated with a light of wavelength 800 nm . The line joining \(A_{1} P\) is perpendicular to \(A_{1} A_{2}\) as shown in the figure.
If the first minimum is detected at \(P\), the value of slits separation '\(a\)' will be the distance of screen from slits \(D = 5\,cm.\)
368091 In young's double slit experiment, the two slits are '\(d\)' distance apart. Interference pattern is observed on the screen at a distance '\(D\)' from the slits. First dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
368093
In a Young's double slit experiment, two slits are illuminated with a light of wavelength 800 nm . The line joining \(A_{1} P\) is perpendicular to \(A_{1} A_{2}\) as shown in the figure.
If the first minimum is detected at \(P\), the value of slits separation '\(a\)' will be the distance of screen from slits \(D = 5\,cm.\)
368091 In young's double slit experiment, the two slits are '\(d\)' distance apart. Interference pattern is observed on the screen at a distance '\(D\)' from the slits. First dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of the light is
368093
In a Young's double slit experiment, two slits are illuminated with a light of wavelength 800 nm . The line joining \(A_{1} P\) is perpendicular to \(A_{1} A_{2}\) as shown in the figure.
If the first minimum is detected at \(P\), the value of slits separation '\(a\)' will be the distance of screen from slits \(D = 5\,cm.\)

