367986
In a typical Young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity \({v=1 {~mm}}\) per second towards the screen, then the instantaneous velocity of central maxima is given as \({\alpha \times 10^{-\beta} {cm} / {s}}\) upward in scientific notation. The value of \({\alpha+\beta}\) is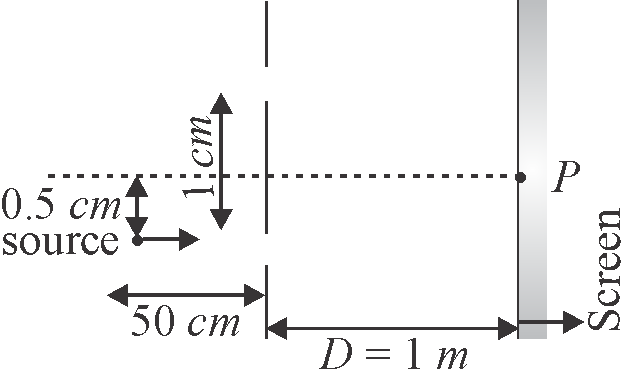
367987
Two circular aperture \({S_{1}}\), and \({S_{2}}\) of radii \(1\,m\) and \(2\,mm\). A parallel beam of light \({\dfrac{7}{22} {Wm}^{-2}}\) and wavelength \(600\,nm\) is incident normally as shown in the figure. A transparent film of thickness \(200\,nm\) having refractive index \({\mu_{1}=2}\) is placed in front of \({S_{1}}\), and other transparent film of thickness \(200\,nm\) and refractive index 1.5 is placed in front of other slit. The resultant power at the centre of screen is
367986
In a typical Young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity \({v=1 {~mm}}\) per second towards the screen, then the instantaneous velocity of central maxima is given as \({\alpha \times 10^{-\beta} {cm} / {s}}\) upward in scientific notation. The value of \({\alpha+\beta}\) is
367987
Two circular aperture \({S_{1}}\), and \({S_{2}}\) of radii \(1\,m\) and \(2\,mm\). A parallel beam of light \({\dfrac{7}{22} {Wm}^{-2}}\) and wavelength \(600\,nm\) is incident normally as shown in the figure. A transparent film of thickness \(200\,nm\) having refractive index \({\mu_{1}=2}\) is placed in front of \({S_{1}}\), and other transparent film of thickness \(200\,nm\) and refractive index 1.5 is placed in front of other slit. The resultant power at the centre of screen is
367986
In a typical Young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity \({v=1 {~mm}}\) per second towards the screen, then the instantaneous velocity of central maxima is given as \({\alpha \times 10^{-\beta} {cm} / {s}}\) upward in scientific notation. The value of \({\alpha+\beta}\) is
367987
Two circular aperture \({S_{1}}\), and \({S_{2}}\) of radii \(1\,m\) and \(2\,mm\). A parallel beam of light \({\dfrac{7}{22} {Wm}^{-2}}\) and wavelength \(600\,nm\) is incident normally as shown in the figure. A transparent film of thickness \(200\,nm\) having refractive index \({\mu_{1}=2}\) is placed in front of \({S_{1}}\), and other transparent film of thickness \(200\,nm\) and refractive index 1.5 is placed in front of other slit. The resultant power at the centre of screen is
367986
In a typical Young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity \({v=1 {~mm}}\) per second towards the screen, then the instantaneous velocity of central maxima is given as \({\alpha \times 10^{-\beta} {cm} / {s}}\) upward in scientific notation. The value of \({\alpha+\beta}\) is
367987
Two circular aperture \({S_{1}}\), and \({S_{2}}\) of radii \(1\,m\) and \(2\,mm\). A parallel beam of light \({\dfrac{7}{22} {Wm}^{-2}}\) and wavelength \(600\,nm\) is incident normally as shown in the figure. A transparent film of thickness \(200\,nm\) having refractive index \({\mu_{1}=2}\) is placed in front of \({S_{1}}\), and other transparent film of thickness \(200\,nm\) and refractive index 1.5 is placed in front of other slit. The resultant power at the centre of screen is