367982
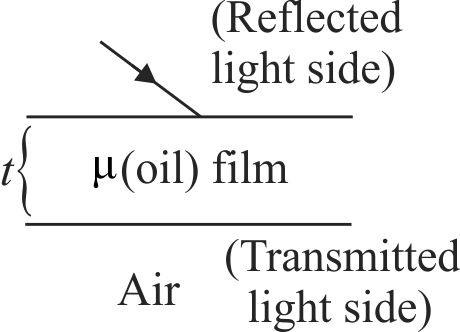
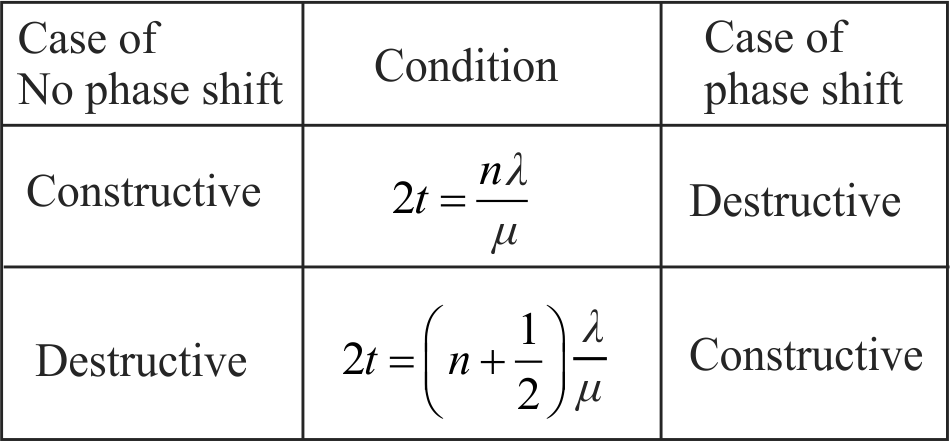
In a modified Young's double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 \( \mathop A^{~~\circ} \) and intensity \({\dfrac{10}{\pi} {W} / {m}^{2}}\) is incident normally on two circular aperture \({A}\) and \({B}\) of radii 0.001 \(m\) and 0.002 \(m\) respectively. A perfect transparent film of thickness 2000\( \mathop A^{~~\circ} \) and refractive index 1.5 for the wavelength of 6000\( \mathop A^{~~\circ} \) is placed in front of aperture \({A}\) as shown in figure.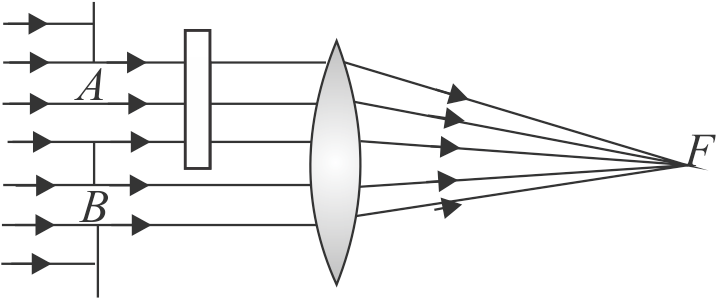
Calculate the intensity of light (in \({\mu {W}}\) ) received at the focal point of the lens in watt. The lens is symmetrically placed with respect to the aperture. Assume that \({10 \%}\) of the power received by each aperture goes in the original direction and is brought to the focal point.
367982
In a modified Young's double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 \( \mathop A^{~~\circ} \) and intensity \({\dfrac{10}{\pi} {W} / {m}^{2}}\) is incident normally on two circular aperture \({A}\) and \({B}\) of radii 0.001 \(m\) and 0.002 \(m\) respectively. A perfect transparent film of thickness 2000\( \mathop A^{~~\circ} \) and refractive index 1.5 for the wavelength of 6000\( \mathop A^{~~\circ} \) is placed in front of aperture \({A}\) as shown in figure.
Calculate the intensity of light (in \({\mu {W}}\) ) received at the focal point of the lens in watt. The lens is symmetrically placed with respect to the aperture. Assume that \({10 \%}\) of the power received by each aperture goes in the original direction and is brought to the focal point.
367982
In a modified Young's double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 \( \mathop A^{~~\circ} \) and intensity \({\dfrac{10}{\pi} {W} / {m}^{2}}\) is incident normally on two circular aperture \({A}\) and \({B}\) of radii 0.001 \(m\) and 0.002 \(m\) respectively. A perfect transparent film of thickness 2000\( \mathop A^{~~\circ} \) and refractive index 1.5 for the wavelength of 6000\( \mathop A^{~~\circ} \) is placed in front of aperture \({A}\) as shown in figure.
Calculate the intensity of light (in \({\mu {W}}\) ) received at the focal point of the lens in watt. The lens is symmetrically placed with respect to the aperture. Assume that \({10 \%}\) of the power received by each aperture goes in the original direction and is brought to the focal point.
367982
In a modified Young's double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 \( \mathop A^{~~\circ} \) and intensity \({\dfrac{10}{\pi} {W} / {m}^{2}}\) is incident normally on two circular aperture \({A}\) and \({B}\) of radii 0.001 \(m\) and 0.002 \(m\) respectively. A perfect transparent film of thickness 2000\( \mathop A^{~~\circ} \) and refractive index 1.5 for the wavelength of 6000\( \mathop A^{~~\circ} \) is placed in front of aperture \({A}\) as shown in figure.
Calculate the intensity of light (in \({\mu {W}}\) ) received at the focal point of the lens in watt. The lens is symmetrically placed with respect to the aperture. Assume that \({10 \%}\) of the power received by each aperture goes in the original direction and is brought to the focal point.
367982
In a modified Young's double slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000 \( \mathop A^{~~\circ} \) and intensity \({\dfrac{10}{\pi} {W} / {m}^{2}}\) is incident normally on two circular aperture \({A}\) and \({B}\) of radii 0.001 \(m\) and 0.002 \(m\) respectively. A perfect transparent film of thickness 2000\( \mathop A^{~~\circ} \) and refractive index 1.5 for the wavelength of 6000\( \mathop A^{~~\circ} \) is placed in front of aperture \({A}\) as shown in figure.
Calculate the intensity of light (in \({\mu {W}}\) ) received at the focal point of the lens in watt. The lens is symmetrically placed with respect to the aperture. Assume that \({10 \%}\) of the power received by each aperture goes in the original direction and is brought to the focal point.