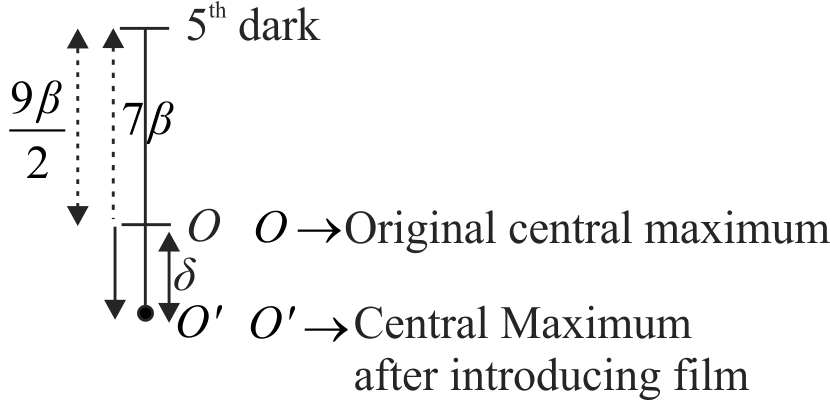
367989 In Young's double slit experiment, \(5^{\text {th }}\) dark fringe is obtained at a point. If a thin transparent film is placed in the path of one of waves, then \(7^{\text {th }}\) bright fringe is obtained at the same point. The thickness of the film in terms of wavelength \(\lambda\) and refractive index \(\mu\) will be
367991 in a Young's double slit experiment, one of the slit is covered with a transparent sheet of thickness \(3.6 \times {10^{ - 3}}\;cm\) due to which position of central fringe shifts to a position originally occupied by 30th bright fringe. The refractive index of the sheet, if \(\lambda = 6000\mathop A\limits^ \circ \) is
367992
A monochromatic beam of light of 6000 \( \mathop A^{~~\circ} \) is used in \(YDSE\) set-up. The two slits are covered with two thin films of equal thickness \({t}\) but of different refractive indices as shown in the figure. Considering the intensity of the incident beam on the slits to be \({I_{0}}\), find the point on the screen at which intensity is \({I_{0}}\) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.)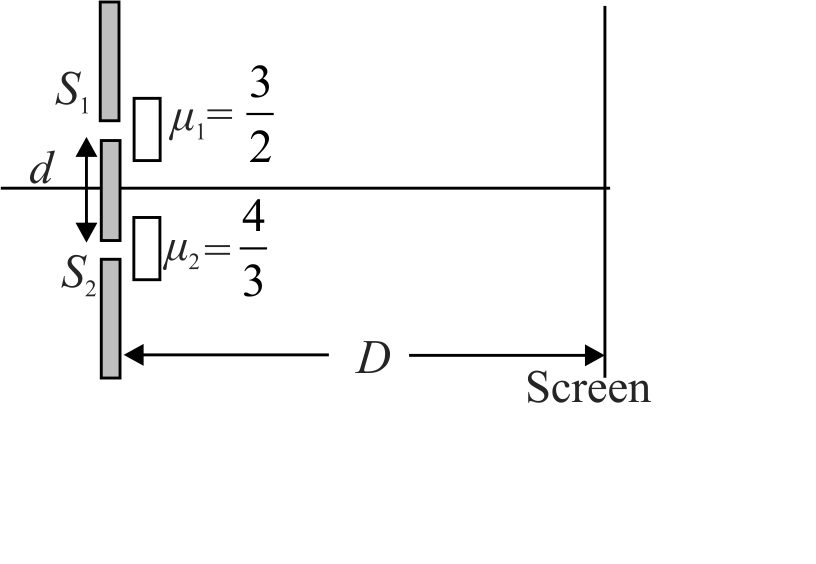
Consider \({t=6 \mu {m}, d=1 {~mm}}\), and \({D=1 {~m}}\), where \({d}\) and \({D}\) have their usual meaning. Give your answer in \(mm\).
367989 In Young's double slit experiment, \(5^{\text {th }}\) dark fringe is obtained at a point. If a thin transparent film is placed in the path of one of waves, then \(7^{\text {th }}\) bright fringe is obtained at the same point. The thickness of the film in terms of wavelength \(\lambda\) and refractive index \(\mu\) will be
367991 in a Young's double slit experiment, one of the slit is covered with a transparent sheet of thickness \(3.6 \times {10^{ - 3}}\;cm\) due to which position of central fringe shifts to a position originally occupied by 30th bright fringe. The refractive index of the sheet, if \(\lambda = 6000\mathop A\limits^ \circ \) is
367992
A monochromatic beam of light of 6000 \( \mathop A^{~~\circ} \) is used in \(YDSE\) set-up. The two slits are covered with two thin films of equal thickness \({t}\) but of different refractive indices as shown in the figure. Considering the intensity of the incident beam on the slits to be \({I_{0}}\), find the point on the screen at which intensity is \({I_{0}}\) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.)
Consider \({t=6 \mu {m}, d=1 {~mm}}\), and \({D=1 {~m}}\), where \({d}\) and \({D}\) have their usual meaning. Give your answer in \(mm\).
367989 In Young's double slit experiment, \(5^{\text {th }}\) dark fringe is obtained at a point. If a thin transparent film is placed in the path of one of waves, then \(7^{\text {th }}\) bright fringe is obtained at the same point. The thickness of the film in terms of wavelength \(\lambda\) and refractive index \(\mu\) will be
367991 in a Young's double slit experiment, one of the slit is covered with a transparent sheet of thickness \(3.6 \times {10^{ - 3}}\;cm\) due to which position of central fringe shifts to a position originally occupied by 30th bright fringe. The refractive index of the sheet, if \(\lambda = 6000\mathop A\limits^ \circ \) is
367992
A monochromatic beam of light of 6000 \( \mathop A^{~~\circ} \) is used in \(YDSE\) set-up. The two slits are covered with two thin films of equal thickness \({t}\) but of different refractive indices as shown in the figure. Considering the intensity of the incident beam on the slits to be \({I_{0}}\), find the point on the screen at which intensity is \({I_{0}}\) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.)
Consider \({t=6 \mu {m}, d=1 {~mm}}\), and \({D=1 {~m}}\), where \({d}\) and \({D}\) have their usual meaning. Give your answer in \(mm\).
367989 In Young's double slit experiment, \(5^{\text {th }}\) dark fringe is obtained at a point. If a thin transparent film is placed in the path of one of waves, then \(7^{\text {th }}\) bright fringe is obtained at the same point. The thickness of the film in terms of wavelength \(\lambda\) and refractive index \(\mu\) will be
367991 in a Young's double slit experiment, one of the slit is covered with a transparent sheet of thickness \(3.6 \times {10^{ - 3}}\;cm\) due to which position of central fringe shifts to a position originally occupied by 30th bright fringe. The refractive index of the sheet, if \(\lambda = 6000\mathop A\limits^ \circ \) is
367992
A monochromatic beam of light of 6000 \( \mathop A^{~~\circ} \) is used in \(YDSE\) set-up. The two slits are covered with two thin films of equal thickness \({t}\) but of different refractive indices as shown in the figure. Considering the intensity of the incident beam on the slits to be \({I_{0}}\), find the point on the screen at which intensity is \({I_{0}}\) and is just above the central maxima. (Assume that there is no change in intensity of the light after passing through the films.)
Consider \({t=6 \mu {m}, d=1 {~mm}}\), and \({D=1 {~m}}\), where \({d}\) and \({D}\) have their usual meaning. Give your answer in \(mm\).