363157
A block of mass \(15\;kg\) is placed at a distance of \(10\;m\) from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is \(0.4.\) Starting from rest, the trolley is given a uniform acceleration of \(5\;m{\rm{/}}{s^2}.\) At what distance (in metres) from the starting point will the block fall-off the trolley? (Take \(g = 10\;m{\rm{/}}{s^2}\))
363159
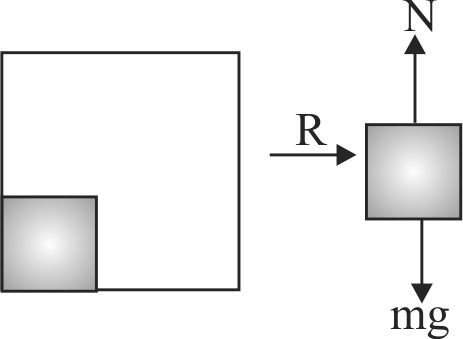
A block of mass 1 \(kg\) rests inside a cubical vessel, as shown in the figure. Which is moving with a velocity of \(v = \sqrt {29} \,t\,\,m/s\) where \(t\) is in sec. All the surfaces are smooth. The block is at rest w.r.t, the cube, what is the total force exerted by the cube on the block?
363157
A block of mass \(15\;kg\) is placed at a distance of \(10\;m\) from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is \(0.4.\) Starting from rest, the trolley is given a uniform acceleration of \(5\;m{\rm{/}}{s^2}.\) At what distance (in metres) from the starting point will the block fall-off the trolley? (Take \(g = 10\;m{\rm{/}}{s^2}\))
363159
A block of mass 1 \(kg\) rests inside a cubical vessel, as shown in the figure. Which is moving with a velocity of \(v = \sqrt {29} \,t\,\,m/s\) where \(t\) is in sec. All the surfaces are smooth. The block is at rest w.r.t, the cube, what is the total force exerted by the cube on the block?
363157
A block of mass \(15\;kg\) is placed at a distance of \(10\;m\) from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is \(0.4.\) Starting from rest, the trolley is given a uniform acceleration of \(5\;m{\rm{/}}{s^2}.\) At what distance (in metres) from the starting point will the block fall-off the trolley? (Take \(g = 10\;m{\rm{/}}{s^2}\))
363159
A block of mass 1 \(kg\) rests inside a cubical vessel, as shown in the figure. Which is moving with a velocity of \(v = \sqrt {29} \,t\,\,m/s\) where \(t\) is in sec. All the surfaces are smooth. The block is at rest w.r.t, the cube, what is the total force exerted by the cube on the block?
363157
A block of mass \(15\;kg\) is placed at a distance of \(10\;m\) from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is \(0.4.\) Starting from rest, the trolley is given a uniform acceleration of \(5\;m{\rm{/}}{s^2}.\) At what distance (in metres) from the starting point will the block fall-off the trolley? (Take \(g = 10\;m{\rm{/}}{s^2}\))
363159
A block of mass 1 \(kg\) rests inside a cubical vessel, as shown in the figure. Which is moving with a velocity of \(v = \sqrt {29} \,t\,\,m/s\) where \(t\) is in sec. All the surfaces are smooth. The block is at rest w.r.t, the cube, what is the total force exerted by the cube on the block?
363157
A block of mass \(15\;kg\) is placed at a distance of \(10\;m\) from the rear end of a long trolley as shown in figure. The coefficient of friction between the block and the surface below is \(0.4.\) Starting from rest, the trolley is given a uniform acceleration of \(5\;m{\rm{/}}{s^2}.\) At what distance (in metres) from the starting point will the block fall-off the trolley? (Take \(g = 10\;m{\rm{/}}{s^2}\))
363159
A block of mass 1 \(kg\) rests inside a cubical vessel, as shown in the figure. Which is moving with a velocity of \(v = \sqrt {29} \,t\,\,m/s\) where \(t\) is in sec. All the surfaces are smooth. The block is at rest w.r.t, the cube, what is the total force exerted by the cube on the block?