354880
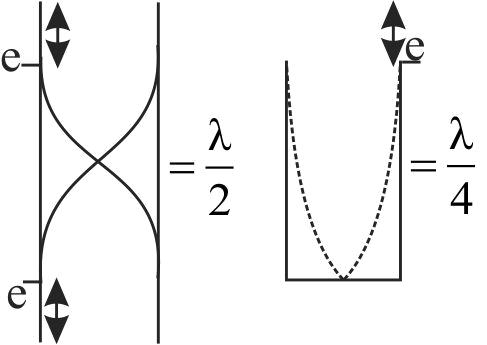
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is
354880
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is
354880
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is
354880
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is
354880
In the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is