366069
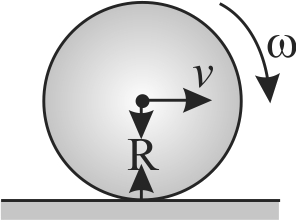
A rigid body is in motion along the path shown. Two points \(P{\rm{ }}\& O\) are considered on the body. \(\alpha\) is the angle made by the axis (that joins \(P\) and \(O\)). w.r.to horizontal direction. If body has to be only in translational motion then.
366069
A rigid body is in motion along the path shown. Two points \(P{\rm{ }}\& O\) are considered on the body. \(\alpha\) is the angle made by the axis (that joins \(P\) and \(O\)). w.r.to horizontal direction. If body has to be only in translational motion then.
366069
A rigid body is in motion along the path shown. Two points \(P{\rm{ }}\& O\) are considered on the body. \(\alpha\) is the angle made by the axis (that joins \(P\) and \(O\)). w.r.to horizontal direction. If body has to be only in translational motion then.
366069
A rigid body is in motion along the path shown. Two points \(P{\rm{ }}\& O\) are considered on the body. \(\alpha\) is the angle made by the axis (that joins \(P\) and \(O\)). w.r.to horizontal direction. If body has to be only in translational motion then.