366063
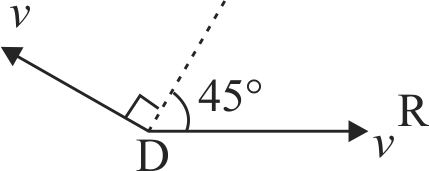
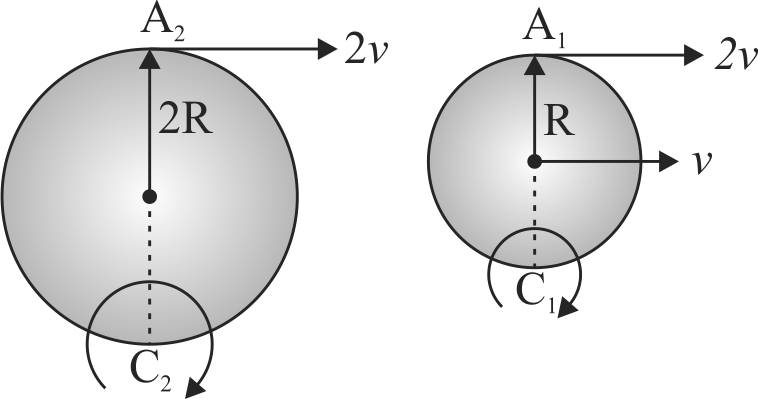
A rigid body is rolling without sliping on the horizontal surface, then match the Column I with Column II and select the correct answer from the codes given below.
Column I
Column II
A
Velocity at point A
P
\(\sqrt 2 v\)
B
Velocity at point B
Q
\(0\)
C
Velocity at point C
R
\(v\sqrt {2 - \sqrt 2 } \)
D
Velocity at point D
S
\(2v\)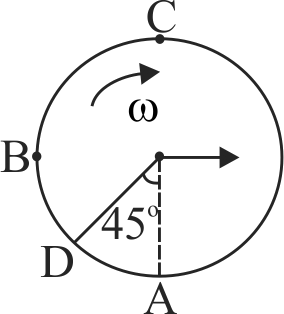
366064
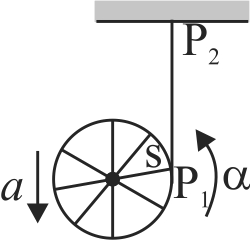
A pulley of radius \(R\) is unwinding with the downward linear acceleration \(a\) and angular acceleration \(\alpha\). If the string is unstretchable and there is no slipping between the string and the pulley, then the relation between \(a\) and \(\alpha\) is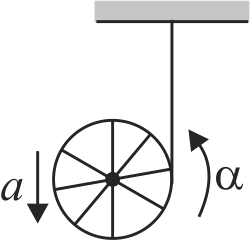
366065
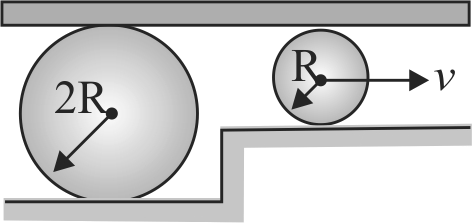
A bobbin is pushed along on a rough stationary horizontal surface as shown in the figure. The board is kept horizontal and there is no slipping at any contact points. The distance moved by the axis of the bobbin is \(l\). The distance travelled by the board \((\mathrm{B})\) is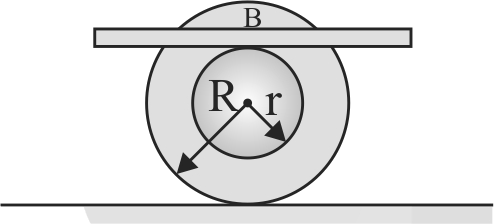
366063
A rigid body is rolling without sliping on the horizontal surface, then match the Column I with Column II and select the correct answer from the codes given below.
Column I
Column II
A
Velocity at point A
P
\(\sqrt 2 v\)
B
Velocity at point B
Q
\(0\)
C
Velocity at point C
R
\(v\sqrt {2 - \sqrt 2 } \)
D
Velocity at point D
S
\(2v\)
366064
A pulley of radius \(R\) is unwinding with the downward linear acceleration \(a\) and angular acceleration \(\alpha\). If the string is unstretchable and there is no slipping between the string and the pulley, then the relation between \(a\) and \(\alpha\) is
366065
A bobbin is pushed along on a rough stationary horizontal surface as shown in the figure. The board is kept horizontal and there is no slipping at any contact points. The distance moved by the axis of the bobbin is \(l\). The distance travelled by the board \((\mathrm{B})\) is
366063
A rigid body is rolling without sliping on the horizontal surface, then match the Column I with Column II and select the correct answer from the codes given below.
Column I
Column II
A
Velocity at point A
P
\(\sqrt 2 v\)
B
Velocity at point B
Q
\(0\)
C
Velocity at point C
R
\(v\sqrt {2 - \sqrt 2 } \)
D
Velocity at point D
S
\(2v\)
366064
A pulley of radius \(R\) is unwinding with the downward linear acceleration \(a\) and angular acceleration \(\alpha\). If the string is unstretchable and there is no slipping between the string and the pulley, then the relation between \(a\) and \(\alpha\) is
366065
A bobbin is pushed along on a rough stationary horizontal surface as shown in the figure. The board is kept horizontal and there is no slipping at any contact points. The distance moved by the axis of the bobbin is \(l\). The distance travelled by the board \((\mathrm{B})\) is
366063
A rigid body is rolling without sliping on the horizontal surface, then match the Column I with Column II and select the correct answer from the codes given below.
Column I
Column II
A
Velocity at point A
P
\(\sqrt 2 v\)
B
Velocity at point B
Q
\(0\)
C
Velocity at point C
R
\(v\sqrt {2 - \sqrt 2 } \)
D
Velocity at point D
S
\(2v\)
366064
A pulley of radius \(R\) is unwinding with the downward linear acceleration \(a\) and angular acceleration \(\alpha\). If the string is unstretchable and there is no slipping between the string and the pulley, then the relation between \(a\) and \(\alpha\) is
366065
A bobbin is pushed along on a rough stationary horizontal surface as shown in the figure. The board is kept horizontal and there is no slipping at any contact points. The distance moved by the axis of the bobbin is \(l\). The distance travelled by the board \((\mathrm{B})\) is