364364
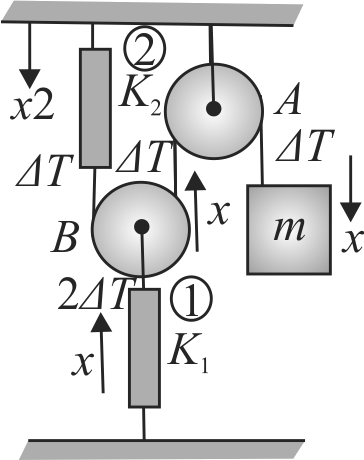
A block of mass \(m\) is tied to one end of a spring which passes over a smooth fixed pulley \(A\) and under a light smooth movable pulley \(B\). The other end of the string is attached to the lower end of a spring of spring constant \(K_{2}\). Find the period of small oscillation of mass \(m\) about its equilibrium position.
(Take \(m=\pi^{2} {~kg}\), \(K_{2}=4 K_{1}\) and\({K_1} = 17{\rm{ }}N/m\).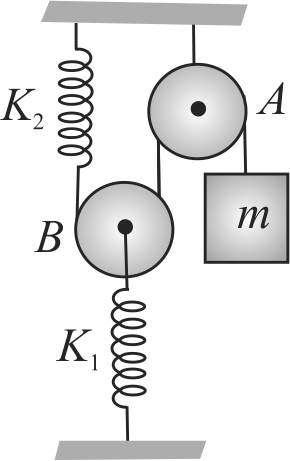
364366
A uniform stick of mass \(M\) and length \(L\) is pivoted at its centre. Its ends are tied to two springs each of force constant \(K\). In the position shown figure, the strings are in their natural length. When the string is displaced through a small angle \(\theta\) and released. The stick: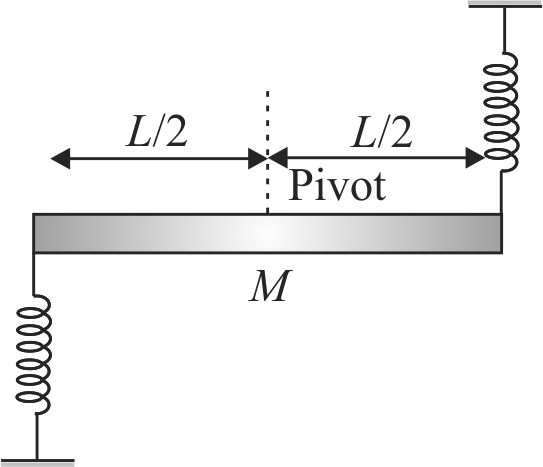
364364
A block of mass \(m\) is tied to one end of a spring which passes over a smooth fixed pulley \(A\) and under a light smooth movable pulley \(B\). The other end of the string is attached to the lower end of a spring of spring constant \(K_{2}\). Find the period of small oscillation of mass \(m\) about its equilibrium position.
(Take \(m=\pi^{2} {~kg}\), \(K_{2}=4 K_{1}\) and\({K_1} = 17{\rm{ }}N/m\).
364366
A uniform stick of mass \(M\) and length \(L\) is pivoted at its centre. Its ends are tied to two springs each of force constant \(K\). In the position shown figure, the strings are in their natural length. When the string is displaced through a small angle \(\theta\) and released. The stick:
364364
A block of mass \(m\) is tied to one end of a spring which passes over a smooth fixed pulley \(A\) and under a light smooth movable pulley \(B\). The other end of the string is attached to the lower end of a spring of spring constant \(K_{2}\). Find the period of small oscillation of mass \(m\) about its equilibrium position.
(Take \(m=\pi^{2} {~kg}\), \(K_{2}=4 K_{1}\) and\({K_1} = 17{\rm{ }}N/m\).
364366
A uniform stick of mass \(M\) and length \(L\) is pivoted at its centre. Its ends are tied to two springs each of force constant \(K\). In the position shown figure, the strings are in their natural length. When the string is displaced through a small angle \(\theta\) and released. The stick:
364364
A block of mass \(m\) is tied to one end of a spring which passes over a smooth fixed pulley \(A\) and under a light smooth movable pulley \(B\). The other end of the string is attached to the lower end of a spring of spring constant \(K_{2}\). Find the period of small oscillation of mass \(m\) about its equilibrium position.
(Take \(m=\pi^{2} {~kg}\), \(K_{2}=4 K_{1}\) and\({K_1} = 17{\rm{ }}N/m\).
364366
A uniform stick of mass \(M\) and length \(L\) is pivoted at its centre. Its ends are tied to two springs each of force constant \(K\). In the position shown figure, the strings are in their natural length. When the string is displaced through a small angle \(\theta\) and released. The stick: