364370
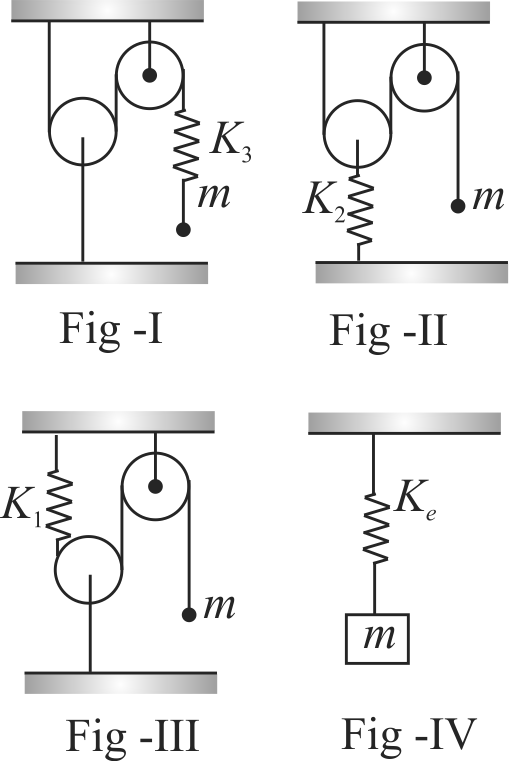
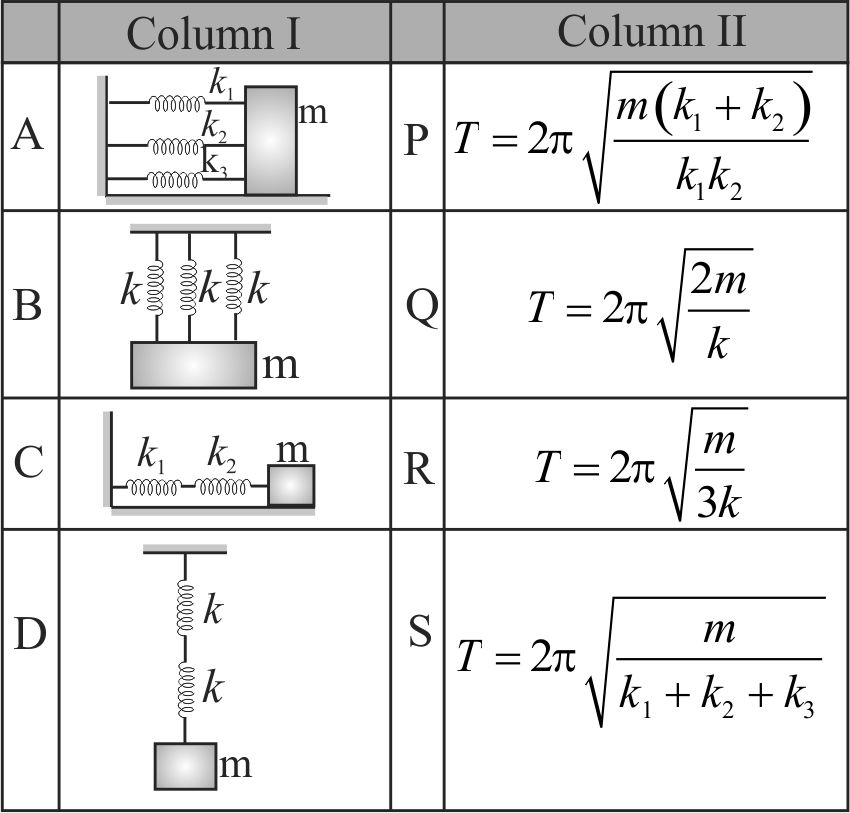
A body of mass \(m\) hangs from a smooth light fixed pulley \(P_{1}\) by the inextensible string fitted with the springs of stiffness \(k_{1}\) and \(k_{2}\). the string passes over the smooth light pulley \(P_{2}\) which is connected with another ideal spring of stiffness \(k_{2}\). Find the period of oscillation of the body.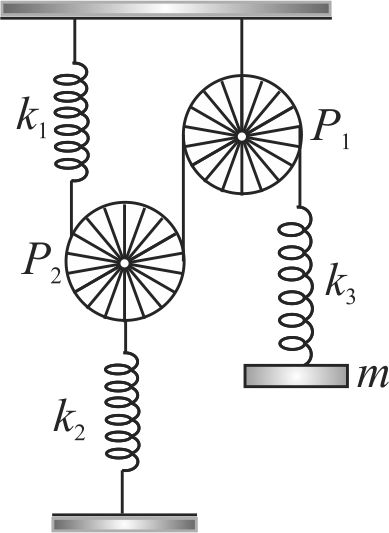
364370
A body of mass \(m\) hangs from a smooth light fixed pulley \(P_{1}\) by the inextensible string fitted with the springs of stiffness \(k_{1}\) and \(k_{2}\). the string passes over the smooth light pulley \(P_{2}\) which is connected with another ideal spring of stiffness \(k_{2}\). Find the period of oscillation of the body.
364370
A body of mass \(m\) hangs from a smooth light fixed pulley \(P_{1}\) by the inextensible string fitted with the springs of stiffness \(k_{1}\) and \(k_{2}\). the string passes over the smooth light pulley \(P_{2}\) which is connected with another ideal spring of stiffness \(k_{2}\). Find the period of oscillation of the body.
364370
A body of mass \(m\) hangs from a smooth light fixed pulley \(P_{1}\) by the inextensible string fitted with the springs of stiffness \(k_{1}\) and \(k_{2}\). the string passes over the smooth light pulley \(P_{2}\) which is connected with another ideal spring of stiffness \(k_{2}\). Find the period of oscillation of the body.
364370
A body of mass \(m\) hangs from a smooth light fixed pulley \(P_{1}\) by the inextensible string fitted with the springs of stiffness \(k_{1}\) and \(k_{2}\). the string passes over the smooth light pulley \(P_{2}\) which is connected with another ideal spring of stiffness \(k_{2}\). Find the period of oscillation of the body.