364361 A \(1\;kg\) block attached to a spring vibrates with a frequency of \(1\;Hz\) on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an \(8\;kg\) block placed on the same table. So, the frequency of vibration of the \(8\;kg\) block is -
364363
Four massless springs whose force constants are \({2 k, 2 k, k}\), and \({2 k}\), respectively are attached to a mass \({M}\), kept on a frictionless plane (as shown in figure). If the mass \({M}\) is displaced in the horizontal direction, then find the frequency of the system.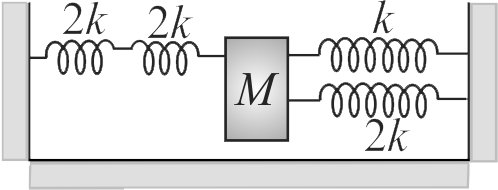
364361 A \(1\;kg\) block attached to a spring vibrates with a frequency of \(1\;Hz\) on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an \(8\;kg\) block placed on the same table. So, the frequency of vibration of the \(8\;kg\) block is -
364363
Four massless springs whose force constants are \({2 k, 2 k, k}\), and \({2 k}\), respectively are attached to a mass \({M}\), kept on a frictionless plane (as shown in figure). If the mass \({M}\) is displaced in the horizontal direction, then find the frequency of the system.
364361 A \(1\;kg\) block attached to a spring vibrates with a frequency of \(1\;Hz\) on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an \(8\;kg\) block placed on the same table. So, the frequency of vibration of the \(8\;kg\) block is -
364363
Four massless springs whose force constants are \({2 k, 2 k, k}\), and \({2 k}\), respectively are attached to a mass \({M}\), kept on a frictionless plane (as shown in figure). If the mass \({M}\) is displaced in the horizontal direction, then find the frequency of the system.
364361 A \(1\;kg\) block attached to a spring vibrates with a frequency of \(1\;Hz\) on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an \(8\;kg\) block placed on the same table. So, the frequency of vibration of the \(8\;kg\) block is -
364363
Four massless springs whose force constants are \({2 k, 2 k, k}\), and \({2 k}\), respectively are attached to a mass \({M}\), kept on a frictionless plane (as shown in figure). If the mass \({M}\) is displaced in the horizontal direction, then find the frequency of the system.