364355
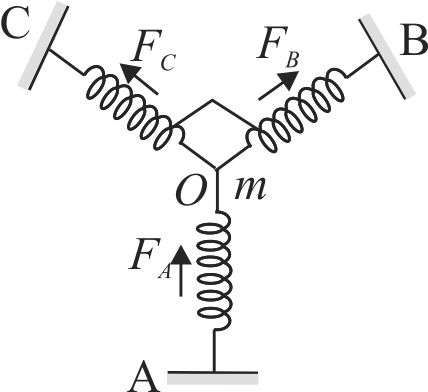
A particle of mass \(m\) is attached to three identical springs \(A,B\) and \(C\) each of force constant \(k\) as shown in figure. If the particle of mass \(m\) is pushed slightly against the spring A and released then the time period of oscillations is (The particle is on a frictionless horizontal surface).
364358
A uniform disc of mass \(m\) and radius \(R\) is connected with two light springs 1 and 2 . The springs are connected at the highest point \(M\) and the \(CM\) ' \(N\) ' of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.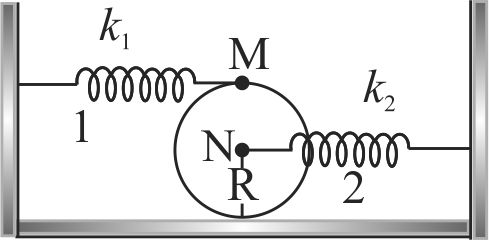
364359
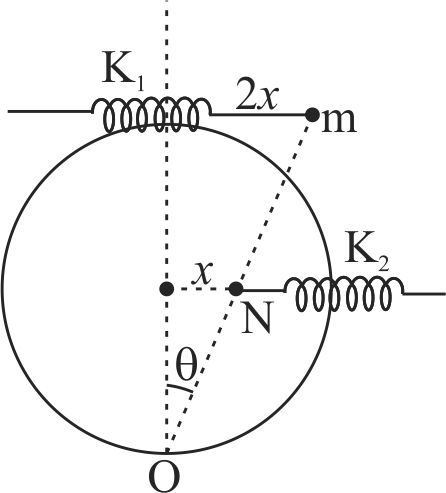
Three identical ideal springs, each of force constant \({k}\) are joined to three identical balls (each of mass \({m}\) ) as shown in the figure. \({O}\) is centroid of the triangle. Initially, each of the springs is in its natural length. Now all the three balls are simultaneously given small displacements of equal magnitude along the directions shown in the figure. The oscillation frequency of balls is \({\dfrac{1}{2 \pi} \sqrt{\dfrac{\beta k}{2 m}}}\). Find the value of \({\beta}\) is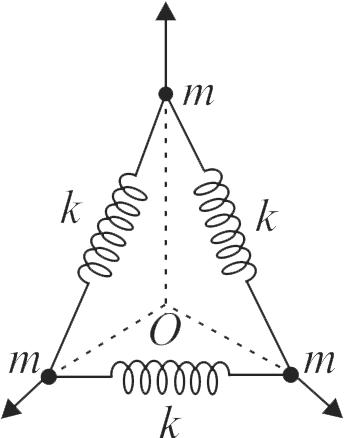
364355
A particle of mass \(m\) is attached to three identical springs \(A,B\) and \(C\) each of force constant \(k\) as shown in figure. If the particle of mass \(m\) is pushed slightly against the spring A and released then the time period of oscillations is (The particle is on a frictionless horizontal surface).
364358
A uniform disc of mass \(m\) and radius \(R\) is connected with two light springs 1 and 2 . The springs are connected at the highest point \(M\) and the \(CM\) ' \(N\) ' of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.
364359
Three identical ideal springs, each of force constant \({k}\) are joined to three identical balls (each of mass \({m}\) ) as shown in the figure. \({O}\) is centroid of the triangle. Initially, each of the springs is in its natural length. Now all the three balls are simultaneously given small displacements of equal magnitude along the directions shown in the figure. The oscillation frequency of balls is \({\dfrac{1}{2 \pi} \sqrt{\dfrac{\beta k}{2 m}}}\). Find the value of \({\beta}\) is
364355
A particle of mass \(m\) is attached to three identical springs \(A,B\) and \(C\) each of force constant \(k\) as shown in figure. If the particle of mass \(m\) is pushed slightly against the spring A and released then the time period of oscillations is (The particle is on a frictionless horizontal surface).
364358
A uniform disc of mass \(m\) and radius \(R\) is connected with two light springs 1 and 2 . The springs are connected at the highest point \(M\) and the \(CM\) ' \(N\) ' of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.
364359
Three identical ideal springs, each of force constant \({k}\) are joined to three identical balls (each of mass \({m}\) ) as shown in the figure. \({O}\) is centroid of the triangle. Initially, each of the springs is in its natural length. Now all the three balls are simultaneously given small displacements of equal magnitude along the directions shown in the figure. The oscillation frequency of balls is \({\dfrac{1}{2 \pi} \sqrt{\dfrac{\beta k}{2 m}}}\). Find the value of \({\beta}\) is
364355
A particle of mass \(m\) is attached to three identical springs \(A,B\) and \(C\) each of force constant \(k\) as shown in figure. If the particle of mass \(m\) is pushed slightly against the spring A and released then the time period of oscillations is (The particle is on a frictionless horizontal surface).
364358
A uniform disc of mass \(m\) and radius \(R\) is connected with two light springs 1 and 2 . The springs are connected at the highest point \(M\) and the \(CM\) ' \(N\) ' of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.
364359
Three identical ideal springs, each of force constant \({k}\) are joined to three identical balls (each of mass \({m}\) ) as shown in the figure. \({O}\) is centroid of the triangle. Initially, each of the springs is in its natural length. Now all the three balls are simultaneously given small displacements of equal magnitude along the directions shown in the figure. The oscillation frequency of balls is \({\dfrac{1}{2 \pi} \sqrt{\dfrac{\beta k}{2 m}}}\). Find the value of \({\beta}\) is
364355
A particle of mass \(m\) is attached to three identical springs \(A,B\) and \(C\) each of force constant \(k\) as shown in figure. If the particle of mass \(m\) is pushed slightly against the spring A and released then the time period of oscillations is (The particle is on a frictionless horizontal surface).
364358
A uniform disc of mass \(m\) and radius \(R\) is connected with two light springs 1 and 2 . The springs are connected at the highest point \(M\) and the \(CM\) ' \(N\) ' of the disc. The other ends of the springs are rigidly attached with vertical walls. If we shift the CM in horizontal by a small distance, the disc oscillates simple harmonically. Assuming a perfect rolling of the disc on the horizontal surface, find the angular frequency of oscillation.
364359
Three identical ideal springs, each of force constant \({k}\) are joined to three identical balls (each of mass \({m}\) ) as shown in the figure. \({O}\) is centroid of the triangle. Initially, each of the springs is in its natural length. Now all the three balls are simultaneously given small displacements of equal magnitude along the directions shown in the figure. The oscillation frequency of balls is \({\dfrac{1}{2 \pi} \sqrt{\dfrac{\beta k}{2 m}}}\). Find the value of \({\beta}\) is