364352
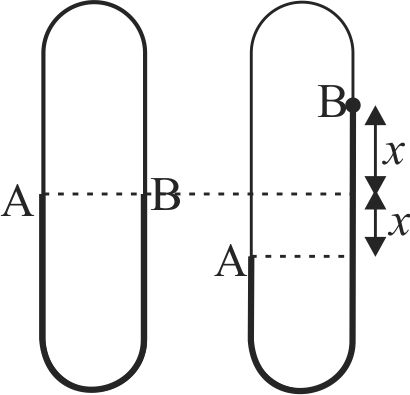
Two uniform ropes having linear mass densities \(m\) and \(4\;m\) are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the figure. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released. It is found that the loop performs SHM with the period of oscillation equal to T. Find the value of
\(T\left( {} \right.\) take \(\left. {l = \frac{{150m}}{{4{\pi ^2}}},g = 10\;m/{s^2}} \right)\).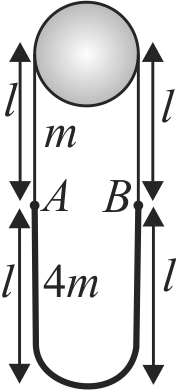
364352
Two uniform ropes having linear mass densities \(m\) and \(4\;m\) are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the figure. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released. It is found that the loop performs SHM with the period of oscillation equal to T. Find the value of
\(T\left( {} \right.\) take \(\left. {l = \frac{{150m}}{{4{\pi ^2}}},g = 10\;m/{s^2}} \right)\).
364352
Two uniform ropes having linear mass densities \(m\) and \(4\;m\) are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the figure. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released. It is found that the loop performs SHM with the period of oscillation equal to T. Find the value of
\(T\left( {} \right.\) take \(\left. {l = \frac{{150m}}{{4{\pi ^2}}},g = 10\;m/{s^2}} \right)\).
364352
Two uniform ropes having linear mass densities \(m\) and \(4\;m\) are joined to form a closed loop. The loop is hanging over a fixed frictionless small pulley with the lighter rope above as shown in the figure. (in the figure equilibrium position is shown). Now if point A (joint) is slightly displaced in downward direction and released. It is found that the loop performs SHM with the period of oscillation equal to T. Find the value of
\(T\left( {} \right.\) take \(\left. {l = \frac{{150m}}{{4{\pi ^2}}},g = 10\;m/{s^2}} \right)\).