364339
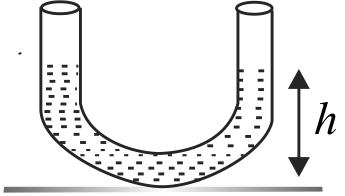
The period of oscillations of mass \({m=200 {~g}}\) poured into a bent tube (see figure), whose right arm makes an angle \({30^{\circ}}\) with the vertical and whose left arm is vertical, is \({T}\) seconds. The cross-sectional area of the tube is \({A=0.5 {~cm}^{2}}\). The value of \({10 T}\) is Neglect viscosity.
364339
The period of oscillations of mass \({m=200 {~g}}\) poured into a bent tube (see figure), whose right arm makes an angle \({30^{\circ}}\) with the vertical and whose left arm is vertical, is \({T}\) seconds. The cross-sectional area of the tube is \({A=0.5 {~cm}^{2}}\). The value of \({10 T}\) is Neglect viscosity.
364339
The period of oscillations of mass \({m=200 {~g}}\) poured into a bent tube (see figure), whose right arm makes an angle \({30^{\circ}}\) with the vertical and whose left arm is vertical, is \({T}\) seconds. The cross-sectional area of the tube is \({A=0.5 {~cm}^{2}}\). The value of \({10 T}\) is Neglect viscosity.
364339
The period of oscillations of mass \({m=200 {~g}}\) poured into a bent tube (see figure), whose right arm makes an angle \({30^{\circ}}\) with the vertical and whose left arm is vertical, is \({T}\) seconds. The cross-sectional area of the tube is \({A=0.5 {~cm}^{2}}\). The value of \({10 T}\) is Neglect viscosity.
364339
The period of oscillations of mass \({m=200 {~g}}\) poured into a bent tube (see figure), whose right arm makes an angle \({30^{\circ}}\) with the vertical and whose left arm is vertical, is \({T}\) seconds. The cross-sectional area of the tube is \({A=0.5 {~cm}^{2}}\). The value of \({10 T}\) is Neglect viscosity.