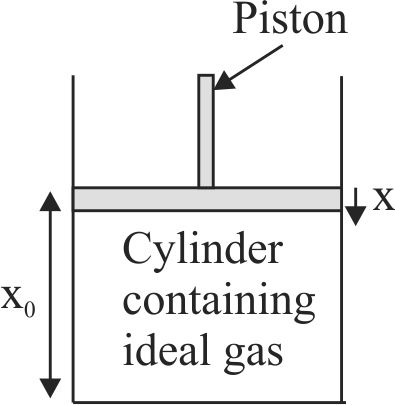
364343 An ideal gas enclosed in a vertical cylinderical container supports a freely moving piston of mass \(M\). The piston and the cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is \(V_{0}\) and its pressure is \(P_{0}\). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

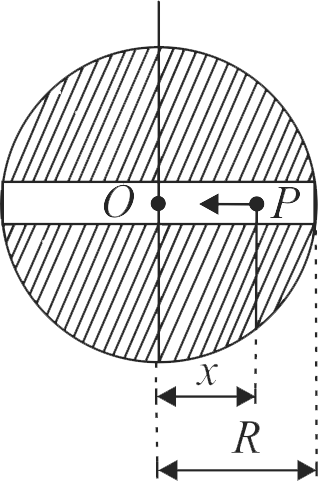
364344 Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in this tunnel, it executes a simple harmonic motion. The mass of the particle is \(100\;g\). The time period of the motion of the particle will be (approximately) (Take \(g = 10\;m{s^{ - 2}}\), radius of earth \( = 6400\;km\))

364345 A uniform cylinder of length \(L\) and mass \(M\) having cross-sectional area \(A\) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density \(\sigma\) at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period \(T\) of the oscillations of the cylinder will be

364346 Assertion :
Water in U-tube executes SHM, the time period for mercury filled up to the same height in the U-tube be greater than that in case of water.
Reason :
The amplitude of the oscillating liquid in U-tube goes on decreasing.

364343 An ideal gas enclosed in a vertical cylinderical container supports a freely moving piston of mass \(M\). The piston and the cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is \(V_{0}\) and its pressure is \(P_{0}\). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

364344 Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in this tunnel, it executes a simple harmonic motion. The mass of the particle is \(100\;g\). The time period of the motion of the particle will be (approximately) (Take \(g = 10\;m{s^{ - 2}}\), radius of earth \( = 6400\;km\))

364345 A uniform cylinder of length \(L\) and mass \(M\) having cross-sectional area \(A\) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density \(\sigma\) at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period \(T\) of the oscillations of the cylinder will be

364346 Assertion :
Water in U-tube executes SHM, the time period for mercury filled up to the same height in the U-tube be greater than that in case of water.
Reason :
The amplitude of the oscillating liquid in U-tube goes on decreasing.

364343 An ideal gas enclosed in a vertical cylinderical container supports a freely moving piston of mass \(M\). The piston and the cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is \(V_{0}\) and its pressure is \(P_{0}\). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

364344 Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in this tunnel, it executes a simple harmonic motion. The mass of the particle is \(100\;g\). The time period of the motion of the particle will be (approximately) (Take \(g = 10\;m{s^{ - 2}}\), radius of earth \( = 6400\;km\))

364345 A uniform cylinder of length \(L\) and mass \(M\) having cross-sectional area \(A\) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density \(\sigma\) at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period \(T\) of the oscillations of the cylinder will be

364346 Assertion :
Water in U-tube executes SHM, the time period for mercury filled up to the same height in the U-tube be greater than that in case of water.
Reason :
The amplitude of the oscillating liquid in U-tube goes on decreasing.

364343 An ideal gas enclosed in a vertical cylinderical container supports a freely moving piston of mass \(M\). The piston and the cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is \(V_{0}\) and its pressure is \(P_{0}\). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

364344 Assume that the earth is a solid sphere of uniform density and a tunnel is dug along its diameter throughout the earth. It is found that when a particle is released in this tunnel, it executes a simple harmonic motion. The mass of the particle is \(100\;g\). The time period of the motion of the particle will be (approximately) (Take \(g = 10\;m{s^{ - 2}}\), radius of earth \( = 6400\;km\))

364345 A uniform cylinder of length \(L\) and mass \(M\) having cross-sectional area \(A\) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density \(\sigma\) at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period \(T\) of the oscillations of the cylinder will be

364346 Assertion :
Water in U-tube executes SHM, the time period for mercury filled up to the same height in the U-tube be greater than that in case of water.
Reason :
The amplitude of the oscillating liquid in U-tube goes on decreasing.