364334
A bead of mass \(m\) can slide on a frictionless wire as shown in figure. Because of the given shape of the wire near \(P\), the bottom point, it can be approximated as a parabola. Near \(P\), the potential energy of the bead is given \(U=c x^{2}\) where \(c\) is a constant and \(x\) is measured from \(P\). The bead, if displaced slightly from point \(P\) will oscillate about \(P\). The period of oscillation is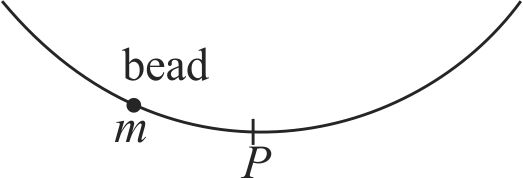
364335 A cylindrical block of wood (density \( = 650\;kg\;{m^{ - 3}}\)), of base area \(30\;c{m^2}\) and height \(54\;cm\), floats in a liquid of density \(900\;kg\;{m^{ - 3}}\). The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly):
364337
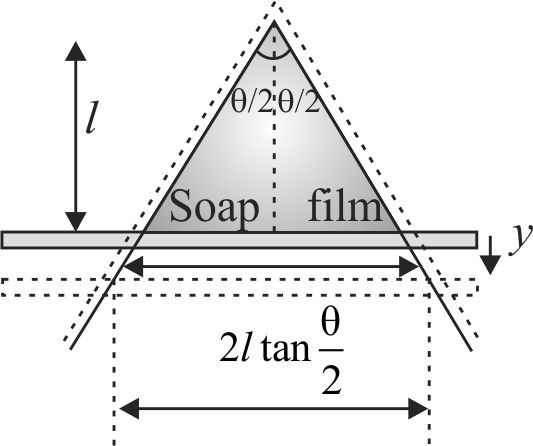
A wire is bent at an angle \(\theta\). A rod of mass \(m\) can slide along the bent wire without friction as shown in Fig. Soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is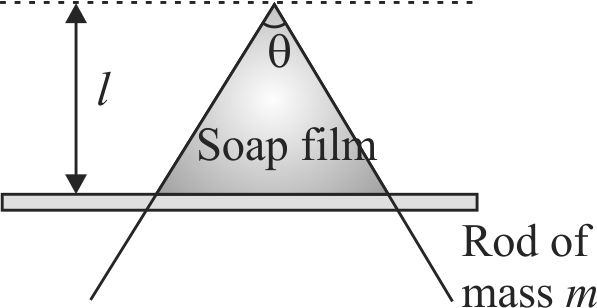
364334
A bead of mass \(m\) can slide on a frictionless wire as shown in figure. Because of the given shape of the wire near \(P\), the bottom point, it can be approximated as a parabola. Near \(P\), the potential energy of the bead is given \(U=c x^{2}\) where \(c\) is a constant and \(x\) is measured from \(P\). The bead, if displaced slightly from point \(P\) will oscillate about \(P\). The period of oscillation is
364335 A cylindrical block of wood (density \( = 650\;kg\;{m^{ - 3}}\)), of base area \(30\;c{m^2}\) and height \(54\;cm\), floats in a liquid of density \(900\;kg\;{m^{ - 3}}\). The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly):
364337
A wire is bent at an angle \(\theta\). A rod of mass \(m\) can slide along the bent wire without friction as shown in Fig. Soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
364334
A bead of mass \(m\) can slide on a frictionless wire as shown in figure. Because of the given shape of the wire near \(P\), the bottom point, it can be approximated as a parabola. Near \(P\), the potential energy of the bead is given \(U=c x^{2}\) where \(c\) is a constant and \(x\) is measured from \(P\). The bead, if displaced slightly from point \(P\) will oscillate about \(P\). The period of oscillation is
364335 A cylindrical block of wood (density \( = 650\;kg\;{m^{ - 3}}\)), of base area \(30\;c{m^2}\) and height \(54\;cm\), floats in a liquid of density \(900\;kg\;{m^{ - 3}}\). The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly):
364337
A wire is bent at an angle \(\theta\). A rod of mass \(m\) can slide along the bent wire without friction as shown in Fig. Soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
364334
A bead of mass \(m\) can slide on a frictionless wire as shown in figure. Because of the given shape of the wire near \(P\), the bottom point, it can be approximated as a parabola. Near \(P\), the potential energy of the bead is given \(U=c x^{2}\) where \(c\) is a constant and \(x\) is measured from \(P\). The bead, if displaced slightly from point \(P\) will oscillate about \(P\). The period of oscillation is
364335 A cylindrical block of wood (density \( = 650\;kg\;{m^{ - 3}}\)), of base area \(30\;c{m^2}\) and height \(54\;cm\), floats in a liquid of density \(900\;kg\;{m^{ - 3}}\). The block is depressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly):
364337
A wire is bent at an angle \(\theta\). A rod of mass \(m\) can slide along the bent wire without friction as shown in Fig. Soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is