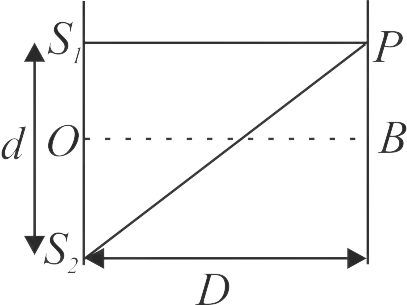
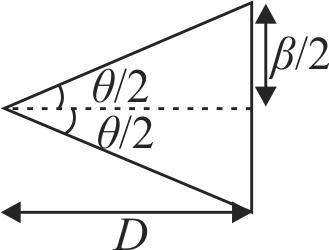
368037 The intensity at the maximum in a Young’s double slit experiment is \({I_0}\) . Distance between two slits is \(d = 5\lambda ,\) where \(\lambda \) is the wavelength of light used in the experiment. What will be the intensity in front of one of the slits on the screen placed at a distance \(D = 10d?\)

368039 Assertion :
All bright interference bands have the same intensity.
Reason :
In interference all bands receive same light from two sources.

368040 Assertion :
One of the condition for interference is that the two sources should be very narrow.
Reason :
One broad source is equal to large number of narrow sources.

368041 In Young’s double slit interference experiment, the distance between two sources is \(0.1/\pi \) \(mm\). The distance of the screen from the source is \(25{\rm{ }}cm.\) Wavelength of light used is \(5000{\rm{ }}\mathop A\limits^ \circ \) Then the angular position of the first dark fringe is

368037 The intensity at the maximum in a Young’s double slit experiment is \({I_0}\) . Distance between two slits is \(d = 5\lambda ,\) where \(\lambda \) is the wavelength of light used in the experiment. What will be the intensity in front of one of the slits on the screen placed at a distance \(D = 10d?\)

368039 Assertion :
All bright interference bands have the same intensity.
Reason :
In interference all bands receive same light from two sources.

368040 Assertion :
One of the condition for interference is that the two sources should be very narrow.
Reason :
One broad source is equal to large number of narrow sources.

368041 In Young’s double slit interference experiment, the distance between two sources is \(0.1/\pi \) \(mm\). The distance of the screen from the source is \(25{\rm{ }}cm.\) Wavelength of light used is \(5000{\rm{ }}\mathop A\limits^ \circ \) Then the angular position of the first dark fringe is

368037 The intensity at the maximum in a Young’s double slit experiment is \({I_0}\) . Distance between two slits is \(d = 5\lambda ,\) where \(\lambda \) is the wavelength of light used in the experiment. What will be the intensity in front of one of the slits on the screen placed at a distance \(D = 10d?\)

368039 Assertion :
All bright interference bands have the same intensity.
Reason :
In interference all bands receive same light from two sources.

368040 Assertion :
One of the condition for interference is that the two sources should be very narrow.
Reason :
One broad source is equal to large number of narrow sources.

368041 In Young’s double slit interference experiment, the distance between two sources is \(0.1/\pi \) \(mm\). The distance of the screen from the source is \(25{\rm{ }}cm.\) Wavelength of light used is \(5000{\rm{ }}\mathop A\limits^ \circ \) Then the angular position of the first dark fringe is

368037 The intensity at the maximum in a Young’s double slit experiment is \({I_0}\) . Distance between two slits is \(d = 5\lambda ,\) where \(\lambda \) is the wavelength of light used in the experiment. What will be the intensity in front of one of the slits on the screen placed at a distance \(D = 10d?\)

368039 Assertion :
All bright interference bands have the same intensity.
Reason :
In interference all bands receive same light from two sources.

368040 Assertion :
One of the condition for interference is that the two sources should be very narrow.
Reason :
One broad source is equal to large number of narrow sources.

368041 In Young’s double slit interference experiment, the distance between two sources is \(0.1/\pi \) \(mm\). The distance of the screen from the source is \(25{\rm{ }}cm.\) Wavelength of light used is \(5000{\rm{ }}\mathop A\limits^ \circ \) Then the angular position of the first dark fringe is