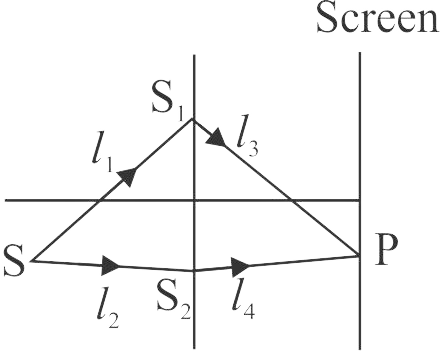
367783
Let \({S_1}\,{\rm{and}}\,{S_2}\) be two sources as shown in the figure.
Which of the following statement \((s)\) is/are correct?
I.
\({S_2}P - {S_1}P = 3\lambda \)
II.
Waves from \({S_1}\) arrives exactly three cycles earlier than waves from \({S_2}\)
III.
At \(P\) waves from \({S_1}{\rm{ and }}{S_2}\) are in phase.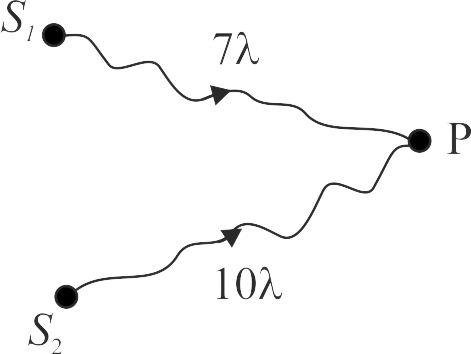
367785 Two light rays having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first ray travels a path \(l_{1}\) through a medium of refractive index \(n_{1}\) while the second ray travels a path of length \(l_{2}\) through a medium of refractive index \(n_{2}\). The two waves are then combined to observe interference. The phase difference between the two waves is
367783
Let \({S_1}\,{\rm{and}}\,{S_2}\) be two sources as shown in the figure.
Which of the following statement \((s)\) is/are correct?
I.
\({S_2}P - {S_1}P = 3\lambda \)
II.
Waves from \({S_1}\) arrives exactly three cycles earlier than waves from \({S_2}\)
III.
At \(P\) waves from \({S_1}{\rm{ and }}{S_2}\) are in phase.
367785 Two light rays having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first ray travels a path \(l_{1}\) through a medium of refractive index \(n_{1}\) while the second ray travels a path of length \(l_{2}\) through a medium of refractive index \(n_{2}\). The two waves are then combined to observe interference. The phase difference between the two waves is
367783
Let \({S_1}\,{\rm{and}}\,{S_2}\) be two sources as shown in the figure.
Which of the following statement \((s)\) is/are correct?
I.
\({S_2}P - {S_1}P = 3\lambda \)
II.
Waves from \({S_1}\) arrives exactly three cycles earlier than waves from \({S_2}\)
III.
At \(P\) waves from \({S_1}{\rm{ and }}{S_2}\) are in phase.
367785 Two light rays having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first ray travels a path \(l_{1}\) through a medium of refractive index \(n_{1}\) while the second ray travels a path of length \(l_{2}\) through a medium of refractive index \(n_{2}\). The two waves are then combined to observe interference. The phase difference between the two waves is
367783
Let \({S_1}\,{\rm{and}}\,{S_2}\) be two sources as shown in the figure.
Which of the following statement \((s)\) is/are correct?
I.
\({S_2}P - {S_1}P = 3\lambda \)
II.
Waves from \({S_1}\) arrives exactly three cycles earlier than waves from \({S_2}\)
III.
At \(P\) waves from \({S_1}{\rm{ and }}{S_2}\) are in phase.
367785 Two light rays having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first ray travels a path \(l_{1}\) through a medium of refractive index \(n_{1}\) while the second ray travels a path of length \(l_{2}\) through a medium of refractive index \(n_{2}\). The two waves are then combined to observe interference. The phase difference between the two waves is
367783
Let \({S_1}\,{\rm{and}}\,{S_2}\) be two sources as shown in the figure.
Which of the following statement \((s)\) is/are correct?
I.
\({S_2}P - {S_1}P = 3\lambda \)
II.
Waves from \({S_1}\) arrives exactly three cycles earlier than waves from \({S_2}\)
III.
At \(P\) waves from \({S_1}{\rm{ and }}{S_2}\) are in phase.
367785 Two light rays having the same wavelength \(\lambda\) in vacuum are in phase initially. Then the first ray travels a path \(l_{1}\) through a medium of refractive index \(n_{1}\) while the second ray travels a path of length \(l_{2}\) through a medium of refractive index \(n_{2}\). The two waves are then combined to observe interference. The phase difference between the two waves is