367785
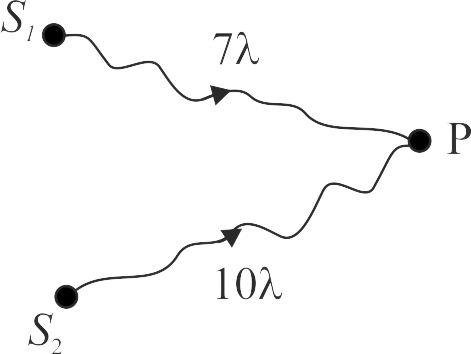
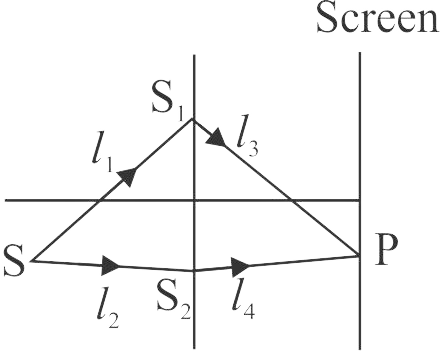
Two light rays having the same wavelength
367785
Two light rays having the same wavelength
367785
Two light rays having the same wavelength
367785
Two light rays having the same wavelength
367785
Two light rays having the same wavelength