366789 A second's pendulum clock has a steel wire. The clock is calibrated at \(20^{\circ} {C}\). How much time does the clock lose or gain in one week when the temperature is increased to \(30^{\circ} {C} ?\left(\alpha_{\text {steel }}=1.2 \times 10^{-5}{ }^{\circ}\,\, {C}^{-1}\right)\).

366790 A pendulum clock loses \(12\;s\) a day if the temperature is \(40^\circ C\) and gains \(4\;s\) a day if the temperature is \(20^\circ C\). The temperature at which the clock will show correct time, and the coefficient of linear expansion \((\alpha)\) of the metal of the pendulum shaft are respectively :

366791 A resistance \(R\) carries a current \(I\). The rate of heat loss to the surroundings is \(\lambda\left(T-T_{0}\right)\) where \(\lambda\) is a constant, \(T\) is the temperature of the resistance, and \(T_{0}\) is the temperature of the atmosphere. If the coefficient of linear expansion is \(\alpha\), the strain in the resistance is :

366792 A steel scale measures the length of a copper wire as \(80.0\;cm\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\) and \({\alpha _{{\rm{copper }}}} = 17 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\))

366793 A steel scale measures the lenght of a copper rod as \(80.0\;cm\;\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the rod when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) and \({\alpha _{{\rm{copper }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) )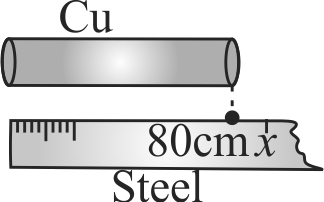

366789 A second's pendulum clock has a steel wire. The clock is calibrated at \(20^{\circ} {C}\). How much time does the clock lose or gain in one week when the temperature is increased to \(30^{\circ} {C} ?\left(\alpha_{\text {steel }}=1.2 \times 10^{-5}{ }^{\circ}\,\, {C}^{-1}\right)\).

366790 A pendulum clock loses \(12\;s\) a day if the temperature is \(40^\circ C\) and gains \(4\;s\) a day if the temperature is \(20^\circ C\). The temperature at which the clock will show correct time, and the coefficient of linear expansion \((\alpha)\) of the metal of the pendulum shaft are respectively :

366791 A resistance \(R\) carries a current \(I\). The rate of heat loss to the surroundings is \(\lambda\left(T-T_{0}\right)\) where \(\lambda\) is a constant, \(T\) is the temperature of the resistance, and \(T_{0}\) is the temperature of the atmosphere. If the coefficient of linear expansion is \(\alpha\), the strain in the resistance is :

366792 A steel scale measures the length of a copper wire as \(80.0\;cm\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\) and \({\alpha _{{\rm{copper }}}} = 17 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\))

366793 A steel scale measures the lenght of a copper rod as \(80.0\;cm\;\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the rod when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) and \({\alpha _{{\rm{copper }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) )

366789 A second's pendulum clock has a steel wire. The clock is calibrated at \(20^{\circ} {C}\). How much time does the clock lose or gain in one week when the temperature is increased to \(30^{\circ} {C} ?\left(\alpha_{\text {steel }}=1.2 \times 10^{-5}{ }^{\circ}\,\, {C}^{-1}\right)\).

366790 A pendulum clock loses \(12\;s\) a day if the temperature is \(40^\circ C\) and gains \(4\;s\) a day if the temperature is \(20^\circ C\). The temperature at which the clock will show correct time, and the coefficient of linear expansion \((\alpha)\) of the metal of the pendulum shaft are respectively :

366791 A resistance \(R\) carries a current \(I\). The rate of heat loss to the surroundings is \(\lambda\left(T-T_{0}\right)\) where \(\lambda\) is a constant, \(T\) is the temperature of the resistance, and \(T_{0}\) is the temperature of the atmosphere. If the coefficient of linear expansion is \(\alpha\), the strain in the resistance is :

366792 A steel scale measures the length of a copper wire as \(80.0\;cm\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\) and \({\alpha _{{\rm{copper }}}} = 17 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\))

366793 A steel scale measures the lenght of a copper rod as \(80.0\;cm\;\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the rod when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) and \({\alpha _{{\rm{copper }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) )

366789 A second's pendulum clock has a steel wire. The clock is calibrated at \(20^{\circ} {C}\). How much time does the clock lose or gain in one week when the temperature is increased to \(30^{\circ} {C} ?\left(\alpha_{\text {steel }}=1.2 \times 10^{-5}{ }^{\circ}\,\, {C}^{-1}\right)\).

366790 A pendulum clock loses \(12\;s\) a day if the temperature is \(40^\circ C\) and gains \(4\;s\) a day if the temperature is \(20^\circ C\). The temperature at which the clock will show correct time, and the coefficient of linear expansion \((\alpha)\) of the metal of the pendulum shaft are respectively :

366791 A resistance \(R\) carries a current \(I\). The rate of heat loss to the surroundings is \(\lambda\left(T-T_{0}\right)\) where \(\lambda\) is a constant, \(T\) is the temperature of the resistance, and \(T_{0}\) is the temperature of the atmosphere. If the coefficient of linear expansion is \(\alpha\), the strain in the resistance is :

366792 A steel scale measures the length of a copper wire as \(80.0\;cm\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\) and \({\alpha _{{\rm{copper }}}} = 17 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\))

366793 A steel scale measures the lenght of a copper rod as \(80.0\;cm\;\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the rod when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) and \({\alpha _{{\rm{copper }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) )

366789 A second's pendulum clock has a steel wire. The clock is calibrated at \(20^{\circ} {C}\). How much time does the clock lose or gain in one week when the temperature is increased to \(30^{\circ} {C} ?\left(\alpha_{\text {steel }}=1.2 \times 10^{-5}{ }^{\circ}\,\, {C}^{-1}\right)\).

366790 A pendulum clock loses \(12\;s\) a day if the temperature is \(40^\circ C\) and gains \(4\;s\) a day if the temperature is \(20^\circ C\). The temperature at which the clock will show correct time, and the coefficient of linear expansion \((\alpha)\) of the metal of the pendulum shaft are respectively :

366791 A resistance \(R\) carries a current \(I\). The rate of heat loss to the surroundings is \(\lambda\left(T-T_{0}\right)\) where \(\lambda\) is a constant, \(T\) is the temperature of the resistance, and \(T_{0}\) is the temperature of the atmosphere. If the coefficient of linear expansion is \(\alpha\), the strain in the resistance is :

366792 A steel scale measures the length of a copper wire as \(80.0\;cm\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the wire when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\) and \({\alpha _{{\rm{copper }}}} = 17 \times {10^{ - 6}}{\mathop{\rm per}\nolimits} \,^\circ C\))

366793 A steel scale measures the lenght of a copper rod as \(80.0\;cm\;\), when both are at \(20^\circ C\) (the calibration temperature for scale). What would be the scale read for the length of the rod when both are at \(40^\circ C\) ? (Given \({\alpha _{{\rm{steel }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) and \({\alpha _{{\rm{copper }}}} = 11 \times {10^{ - 6}}{\rm{per }}^\circ C\) )