366785 A clock while keeps correct time at \( 30^\circ C\) has a pendulum rod made of brass. The number of seconds it gains (or) loses per second when the temperature falls to \( 10^\circ C\) is
\(\left[\alpha\right.\) brass \(\left. { = 18 \times {{10}^{ - 6}}/^\circ C} \right]\)

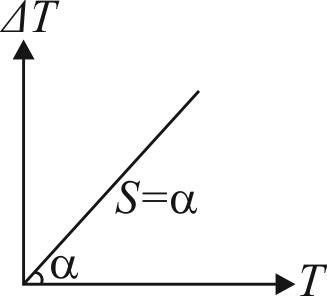
366786 A simple pendulum made of a bob of mass \(m\) and a metallic wire of negligible mass has time period \(2\;s\) at \(T = 0^\circ C\). If the temperature of the wire is increased and the corresponding change in its time period is plotted against its temperature, the resulting graph is a line of slop \(S\). If the coefficient of linear expansion of metal is \(\alpha\) then the value of \(S\) is :

366787 On a linear temperature scale \(Y\), water freezes at \( - 160^\circ Y\) and boils at \( - 500^\circ Y\). On this Y scale, a temperature of \(340\;K\) would be read as: (Water freezes at \(273\;K\) and boils at \(373\;K\))

366788 A clock with a metal pendulum beating seconds keeps correct time at \(0^\circ C\). If it loses \(12.5\;s\) a day at \(25^\circ C\), the coefficient of linear expansion of metal of pendulum is

366785 A clock while keeps correct time at \( 30^\circ C\) has a pendulum rod made of brass. The number of seconds it gains (or) loses per second when the temperature falls to \( 10^\circ C\) is
\(\left[\alpha\right.\) brass \(\left. { = 18 \times {{10}^{ - 6}}/^\circ C} \right]\)

366786 A simple pendulum made of a bob of mass \(m\) and a metallic wire of negligible mass has time period \(2\;s\) at \(T = 0^\circ C\). If the temperature of the wire is increased and the corresponding change in its time period is plotted against its temperature, the resulting graph is a line of slop \(S\). If the coefficient of linear expansion of metal is \(\alpha\) then the value of \(S\) is :

366787 On a linear temperature scale \(Y\), water freezes at \( - 160^\circ Y\) and boils at \( - 500^\circ Y\). On this Y scale, a temperature of \(340\;K\) would be read as: (Water freezes at \(273\;K\) and boils at \(373\;K\))

366788 A clock with a metal pendulum beating seconds keeps correct time at \(0^\circ C\). If it loses \(12.5\;s\) a day at \(25^\circ C\), the coefficient of linear expansion of metal of pendulum is

366785 A clock while keeps correct time at \( 30^\circ C\) has a pendulum rod made of brass. The number of seconds it gains (or) loses per second when the temperature falls to \( 10^\circ C\) is
\(\left[\alpha\right.\) brass \(\left. { = 18 \times {{10}^{ - 6}}/^\circ C} \right]\)

366786 A simple pendulum made of a bob of mass \(m\) and a metallic wire of negligible mass has time period \(2\;s\) at \(T = 0^\circ C\). If the temperature of the wire is increased and the corresponding change in its time period is plotted against its temperature, the resulting graph is a line of slop \(S\). If the coefficient of linear expansion of metal is \(\alpha\) then the value of \(S\) is :

366787 On a linear temperature scale \(Y\), water freezes at \( - 160^\circ Y\) and boils at \( - 500^\circ Y\). On this Y scale, a temperature of \(340\;K\) would be read as: (Water freezes at \(273\;K\) and boils at \(373\;K\))

366788 A clock with a metal pendulum beating seconds keeps correct time at \(0^\circ C\). If it loses \(12.5\;s\) a day at \(25^\circ C\), the coefficient of linear expansion of metal of pendulum is

366785 A clock while keeps correct time at \( 30^\circ C\) has a pendulum rod made of brass. The number of seconds it gains (or) loses per second when the temperature falls to \( 10^\circ C\) is
\(\left[\alpha\right.\) brass \(\left. { = 18 \times {{10}^{ - 6}}/^\circ C} \right]\)

366786 A simple pendulum made of a bob of mass \(m\) and a metallic wire of negligible mass has time period \(2\;s\) at \(T = 0^\circ C\). If the temperature of the wire is increased and the corresponding change in its time period is plotted against its temperature, the resulting graph is a line of slop \(S\). If the coefficient of linear expansion of metal is \(\alpha\) then the value of \(S\) is :

366787 On a linear temperature scale \(Y\), water freezes at \( - 160^\circ Y\) and boils at \( - 500^\circ Y\). On this Y scale, a temperature of \(340\;K\) would be read as: (Water freezes at \(273\;K\) and boils at \(373\;K\))

366788 A clock with a metal pendulum beating seconds keeps correct time at \(0^\circ C\). If it loses \(12.5\;s\) a day at \(25^\circ C\), the coefficient of linear expansion of metal of pendulum is