366781 A steel meter scale is to be ruled so that millimeter intervals are accurate within about \(5 \times {10^{ - 5}}\;mm\) at a certain temperature. The maximum temperature variation allowable during the ruling is (Coefficient of linear expansion of steel \( = 10 \times {10^{ - 6}}\;{K^{ - 1}})\)
366782
A planar frame made of thin uniform rods, the length of section \(A B\) and \(E F\) is \(l_{1}\) and its thermal linear coefficient of expansion is \(\alpha_{1}\). The length of section \(C D\) is \(l_{2}\) and its thermal linear coefficient of expansion is \(\alpha_{2} . C B\) and \(D E\) are of same length having thermal linear coefficient of expansion \(\alpha_{2}\). Points \(A, B, E\) and \(F\) reside on same line, that is, sections \(A B\) and \(E F\) overlap. Then the ratio of \(\dfrac{l_{1}}{l_{2}}\), for which the distance between end \(A\) and \(F\) remains the same at all temperatures, is:
366783
Two scales having different coefficients of linear expansion are caliberated at room temperature. Now the temperature of the scales are increased by \(20^\circ C\) then \(15\;cm\) mark of first scale coincides with \(12\;cm\) mark of second scale. Find the mark on first scale that coincides with \(10\;cm\) mark on second scale.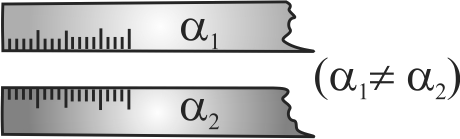
366781 A steel meter scale is to be ruled so that millimeter intervals are accurate within about \(5 \times {10^{ - 5}}\;mm\) at a certain temperature. The maximum temperature variation allowable during the ruling is (Coefficient of linear expansion of steel \( = 10 \times {10^{ - 6}}\;{K^{ - 1}})\)
366782
A planar frame made of thin uniform rods, the length of section \(A B\) and \(E F\) is \(l_{1}\) and its thermal linear coefficient of expansion is \(\alpha_{1}\). The length of section \(C D\) is \(l_{2}\) and its thermal linear coefficient of expansion is \(\alpha_{2} . C B\) and \(D E\) are of same length having thermal linear coefficient of expansion \(\alpha_{2}\). Points \(A, B, E\) and \(F\) reside on same line, that is, sections \(A B\) and \(E F\) overlap. Then the ratio of \(\dfrac{l_{1}}{l_{2}}\), for which the distance between end \(A\) and \(F\) remains the same at all temperatures, is:
366783
Two scales having different coefficients of linear expansion are caliberated at room temperature. Now the temperature of the scales are increased by \(20^\circ C\) then \(15\;cm\) mark of first scale coincides with \(12\;cm\) mark of second scale. Find the mark on first scale that coincides with \(10\;cm\) mark on second scale.
366781 A steel meter scale is to be ruled so that millimeter intervals are accurate within about \(5 \times {10^{ - 5}}\;mm\) at a certain temperature. The maximum temperature variation allowable during the ruling is (Coefficient of linear expansion of steel \( = 10 \times {10^{ - 6}}\;{K^{ - 1}})\)
366782
A planar frame made of thin uniform rods, the length of section \(A B\) and \(E F\) is \(l_{1}\) and its thermal linear coefficient of expansion is \(\alpha_{1}\). The length of section \(C D\) is \(l_{2}\) and its thermal linear coefficient of expansion is \(\alpha_{2} . C B\) and \(D E\) are of same length having thermal linear coefficient of expansion \(\alpha_{2}\). Points \(A, B, E\) and \(F\) reside on same line, that is, sections \(A B\) and \(E F\) overlap. Then the ratio of \(\dfrac{l_{1}}{l_{2}}\), for which the distance between end \(A\) and \(F\) remains the same at all temperatures, is:
366783
Two scales having different coefficients of linear expansion are caliberated at room temperature. Now the temperature of the scales are increased by \(20^\circ C\) then \(15\;cm\) mark of first scale coincides with \(12\;cm\) mark of second scale. Find the mark on first scale that coincides with \(10\;cm\) mark on second scale.
366781 A steel meter scale is to be ruled so that millimeter intervals are accurate within about \(5 \times {10^{ - 5}}\;mm\) at a certain temperature. The maximum temperature variation allowable during the ruling is (Coefficient of linear expansion of steel \( = 10 \times {10^{ - 6}}\;{K^{ - 1}})\)
366782
A planar frame made of thin uniform rods, the length of section \(A B\) and \(E F\) is \(l_{1}\) and its thermal linear coefficient of expansion is \(\alpha_{1}\). The length of section \(C D\) is \(l_{2}\) and its thermal linear coefficient of expansion is \(\alpha_{2} . C B\) and \(D E\) are of same length having thermal linear coefficient of expansion \(\alpha_{2}\). Points \(A, B, E\) and \(F\) reside on same line, that is, sections \(A B\) and \(E F\) overlap. Then the ratio of \(\dfrac{l_{1}}{l_{2}}\), for which the distance between end \(A\) and \(F\) remains the same at all temperatures, is:
366783
Two scales having different coefficients of linear expansion are caliberated at room temperature. Now the temperature of the scales are increased by \(20^\circ C\) then \(15\;cm\) mark of first scale coincides with \(12\;cm\) mark of second scale. Find the mark on first scale that coincides with \(10\;cm\) mark on second scale.
