363680
The above is a plot of binding energy per nucleon \({E_b},\) against the nuclear mass \(M;A,\,B,\,C,\,D,\,E\,\& \,F\) correspond to different nuclei. Consider four reactions
\((i)A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,(ii)C \to A + B + \varepsilon \)
\((iii){\rm{ }}D + E \to F + \varepsilon {\rm{ }}\,\,(iv){\rm{ }}F \to D + E + \varepsilon \)
Where \(\varepsilon \) is the energy released? In which reactions is \(\varepsilon \) positive?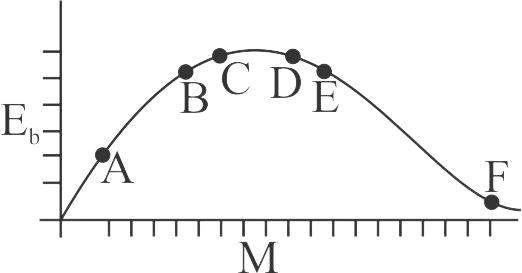
363680
The above is a plot of binding energy per nucleon \({E_b},\) against the nuclear mass \(M;A,\,B,\,C,\,D,\,E\,\& \,F\) correspond to different nuclei. Consider four reactions
\((i)A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,(ii)C \to A + B + \varepsilon \)
\((iii){\rm{ }}D + E \to F + \varepsilon {\rm{ }}\,\,(iv){\rm{ }}F \to D + E + \varepsilon \)
Where \(\varepsilon \) is the energy released? In which reactions is \(\varepsilon \) positive?
363680
The above is a plot of binding energy per nucleon \({E_b},\) against the nuclear mass \(M;A,\,B,\,C,\,D,\,E\,\& \,F\) correspond to different nuclei. Consider four reactions
\((i)A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,(ii)C \to A + B + \varepsilon \)
\((iii){\rm{ }}D + E \to F + \varepsilon {\rm{ }}\,\,(iv){\rm{ }}F \to D + E + \varepsilon \)
Where \(\varepsilon \) is the energy released? In which reactions is \(\varepsilon \) positive?
363680
The above is a plot of binding energy per nucleon \({E_b},\) against the nuclear mass \(M;A,\,B,\,C,\,D,\,E\,\& \,F\) correspond to different nuclei. Consider four reactions
\((i)A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,(ii)C \to A + B + \varepsilon \)
\((iii){\rm{ }}D + E \to F + \varepsilon {\rm{ }}\,\,(iv){\rm{ }}F \to D + E + \varepsilon \)
Where \(\varepsilon \) is the energy released? In which reactions is \(\varepsilon \) positive?
363680
The above is a plot of binding energy per nucleon \({E_b},\) against the nuclear mass \(M;A,\,B,\,C,\,D,\,E\,\& \,F\) correspond to different nuclei. Consider four reactions
\((i)A + B \to C + \varepsilon \,\,\,\,\,\,\,\,\,\,(ii)C \to A + B + \varepsilon \)
\((iii){\rm{ }}D + E \to F + \varepsilon {\rm{ }}\,\,(iv){\rm{ }}F \to D + E + \varepsilon \)
Where \(\varepsilon \) is the energy released? In which reactions is \(\varepsilon \) positive?