Explanation:
Given \(t_{\text {rough }}=n t_{\text {smooth }}\)
\(\Rightarrow t_{2}=n t_{1}\)
Let the coefficient of kinetic friction is \(\mu\).
For smooth surface:
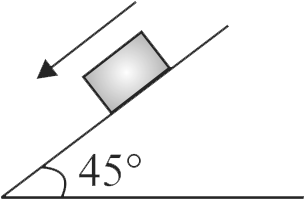
acceleration \(a_{1}=g \sin \theta=g \sin 45^{\circ}=g / \sqrt{2}\)
Let the length of path is \(S\) and time taken to slide down is \(t_{1} S=0+\dfrac{1}{2} \times \dfrac{g}{\sqrt{2}} t_{1}^{2}\)
\(S = \frac{g}{{2\sqrt 2 }}t_1^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
For rough surface :
\(a_{2}=g \sin \theta-\mu g \cos \theta=\dfrac{1}{\sqrt{2}} g(1-\mu)\)
\(\therefore S=0+\dfrac{1}{2} \cdot a_{2} \cdot t_{2}^{2}\)
\(S = \frac{1}{{2\sqrt 2 }}g(1 - \mu )t_2^2\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
From (1) and (2),
\(\dfrac{g}{2 \sqrt{2}} t_{1}^{2}=\dfrac{g}{2 \sqrt{2}}(1-\mu) t_{2}^{2}\)
\(\Rightarrow \quad t_{1}^{2}=(1-\mu) \times n^{2} \times t_{1}^{2} \quad\) As, \(\left[t_{2}=n t_{1}\right]\)
\(\dfrac{1}{n^{2}}=1-\mu ; \Rightarrow \mu=1-\dfrac{1}{n^{2}}\)