363365 A given object takes \(n\) times the time to slide down \(45^{\circ}\) rough inclined plane as it takes the time to slide down an identical perfectly smooth \(45^{\circ}\) inclined plane. The coefficient of kinetic friction between the object and the surface of inclined plane is
363366
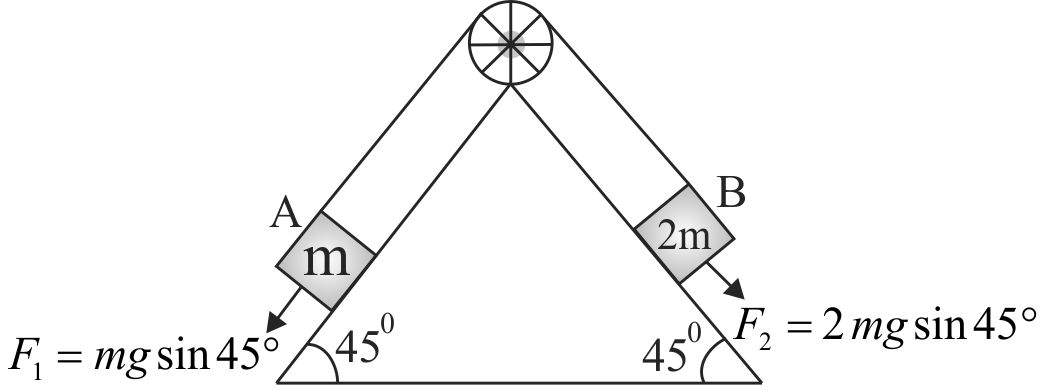
Block \(A\) of mass \(m\) and block \(B\) of mass 2 \(m\) are placed on a fixed triangular wedge by means of massless, inextensible string and a frictionless pulley as shown. The wedge is inclined at \(45^\circ \) to horizontal on both sides. The coefficient of friction between block \(A\) and wedge is 2/3 and between block \(B\) and wedge is 1/3. If system of \(A\) and \(B\) is released from rest then acceleration of \(A\) is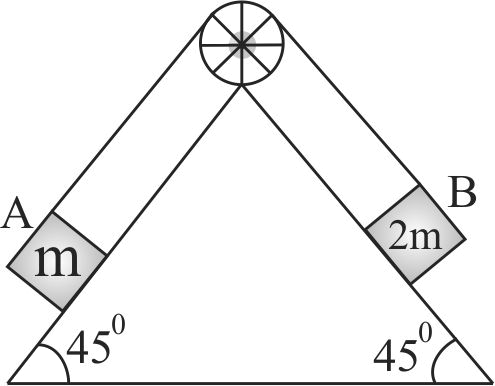
363368
Two blocks of masses \({m_{1}=m_{2}=m}\) are connected by a string of negligible mass, which passes over a frictionless pulley connected with a plane, as shown in the figure. When the inclination \({\theta=45^{\circ}}\), the mass \({m_{1}}\) begins to move up the inclined plane. What is the coefficient of friction between block \({m_{1}}\) and the inclined planes?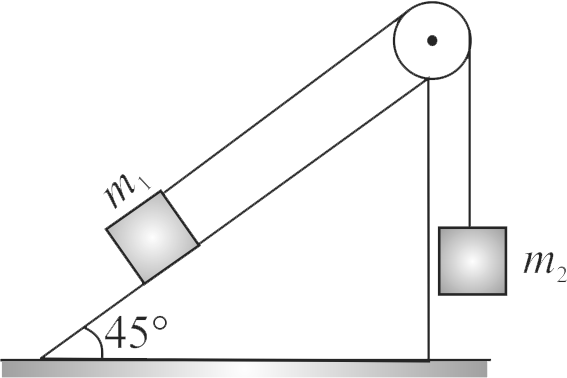
363365 A given object takes \(n\) times the time to slide down \(45^{\circ}\) rough inclined plane as it takes the time to slide down an identical perfectly smooth \(45^{\circ}\) inclined plane. The coefficient of kinetic friction between the object and the surface of inclined plane is
363366
Block \(A\) of mass \(m\) and block \(B\) of mass 2 \(m\) are placed on a fixed triangular wedge by means of massless, inextensible string and a frictionless pulley as shown. The wedge is inclined at \(45^\circ \) to horizontal on both sides. The coefficient of friction between block \(A\) and wedge is 2/3 and between block \(B\) and wedge is 1/3. If system of \(A\) and \(B\) is released from rest then acceleration of \(A\) is
363368
Two blocks of masses \({m_{1}=m_{2}=m}\) are connected by a string of negligible mass, which passes over a frictionless pulley connected with a plane, as shown in the figure. When the inclination \({\theta=45^{\circ}}\), the mass \({m_{1}}\) begins to move up the inclined plane. What is the coefficient of friction between block \({m_{1}}\) and the inclined planes?
363365 A given object takes \(n\) times the time to slide down \(45^{\circ}\) rough inclined plane as it takes the time to slide down an identical perfectly smooth \(45^{\circ}\) inclined plane. The coefficient of kinetic friction between the object and the surface of inclined plane is
363366
Block \(A\) of mass \(m\) and block \(B\) of mass 2 \(m\) are placed on a fixed triangular wedge by means of massless, inextensible string and a frictionless pulley as shown. The wedge is inclined at \(45^\circ \) to horizontal on both sides. The coefficient of friction between block \(A\) and wedge is 2/3 and between block \(B\) and wedge is 1/3. If system of \(A\) and \(B\) is released from rest then acceleration of \(A\) is
363368
Two blocks of masses \({m_{1}=m_{2}=m}\) are connected by a string of negligible mass, which passes over a frictionless pulley connected with a plane, as shown in the figure. When the inclination \({\theta=45^{\circ}}\), the mass \({m_{1}}\) begins to move up the inclined plane. What is the coefficient of friction between block \({m_{1}}\) and the inclined planes?
363365 A given object takes \(n\) times the time to slide down \(45^{\circ}\) rough inclined plane as it takes the time to slide down an identical perfectly smooth \(45^{\circ}\) inclined plane. The coefficient of kinetic friction between the object and the surface of inclined plane is
363366
Block \(A\) of mass \(m\) and block \(B\) of mass 2 \(m\) are placed on a fixed triangular wedge by means of massless, inextensible string and a frictionless pulley as shown. The wedge is inclined at \(45^\circ \) to horizontal on both sides. The coefficient of friction between block \(A\) and wedge is 2/3 and between block \(B\) and wedge is 1/3. If system of \(A\) and \(B\) is released from rest then acceleration of \(A\) is
363368
Two blocks of masses \({m_{1}=m_{2}=m}\) are connected by a string of negligible mass, which passes over a frictionless pulley connected with a plane, as shown in the figure. When the inclination \({\theta=45^{\circ}}\), the mass \({m_{1}}\) begins to move up the inclined plane. What is the coefficient of friction between block \({m_{1}}\) and the inclined planes?