363303
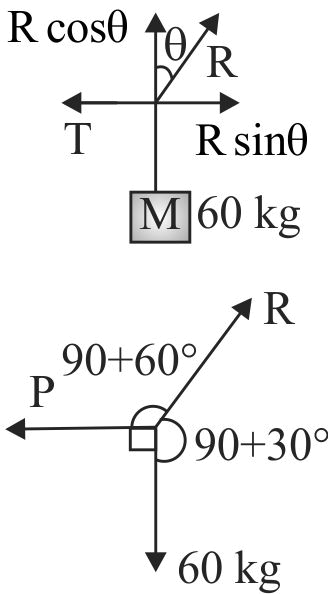
The block is in equilibrium:
\((i)\,\,{T_1} = \frac{{mg\cos \beta }}{{\sin (\alpha + \beta )}}\,\,\,\,\,\,\,\,(ii)\,\,{T_2} = \frac{{mg\cos \alpha }}{{\sin (\alpha + \beta )}}\)
\((iii)\,\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \beta }}{{\cos \alpha }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(iv)\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \alpha }}{{\cos \beta }}\)
Find the correct option
363303
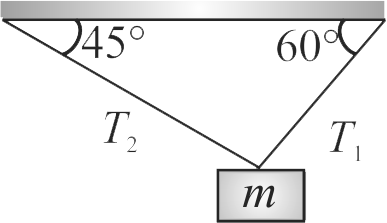
The block is in equilibrium:
\((i)\,\,{T_1} = \frac{{mg\cos \beta }}{{\sin (\alpha + \beta )}}\,\,\,\,\,\,\,\,(ii)\,\,{T_2} = \frac{{mg\cos \alpha }}{{\sin (\alpha + \beta )}}\)
\((iii)\,\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \beta }}{{\cos \alpha }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(iv)\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \alpha }}{{\cos \beta }}\)
Find the correct option
363303
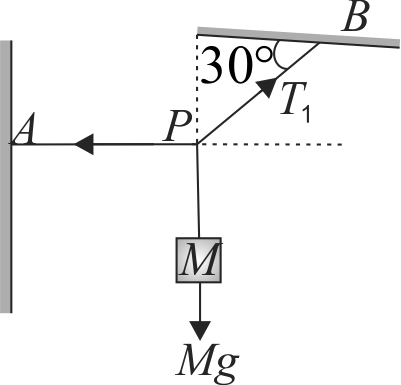
The block is in equilibrium:
\((i)\,\,{T_1} = \frac{{mg\cos \beta }}{{\sin (\alpha + \beta )}}\,\,\,\,\,\,\,\,(ii)\,\,{T_2} = \frac{{mg\cos \alpha }}{{\sin (\alpha + \beta )}}\)
\((iii)\,\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \beta }}{{\cos \alpha }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(iv)\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \alpha }}{{\cos \beta }}\)
Find the correct option
363303
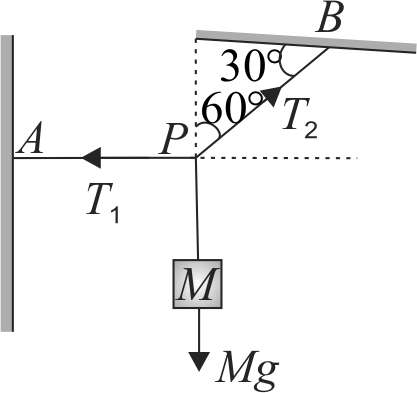
The block is in equilibrium:
\((i)\,\,{T_1} = \frac{{mg\cos \beta }}{{\sin (\alpha + \beta )}}\,\,\,\,\,\,\,\,(ii)\,\,{T_2} = \frac{{mg\cos \alpha }}{{\sin (\alpha + \beta )}}\)
\((iii)\,\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \beta }}{{\cos \alpha }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(iv)\,\frac{{{T_1}}}{{{T_2}}} = \frac{{\cos \alpha }}{{\cos \beta }}\)
Find the correct option