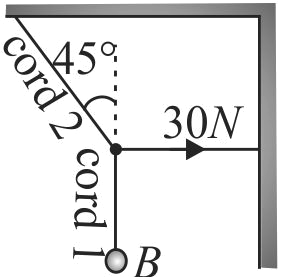
363308 A steel wire can withstand a load upto \(2940\;N\). A load of \(150\;kg\) is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passes through the position of equilibrium, is
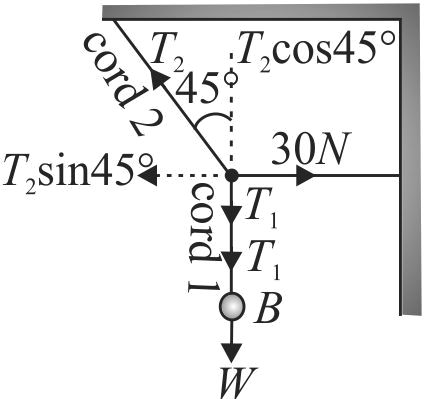
363308 A steel wire can withstand a load upto \(2940\;N\). A load of \(150\;kg\) is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passes through the position of equilibrium, is
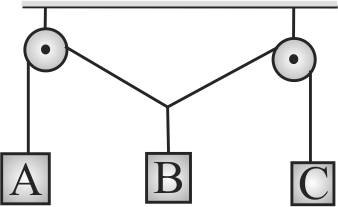
363308 A steel wire can withstand a load upto \(2940\;N\). A load of \(150\;kg\) is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passes through the position of equilibrium, is
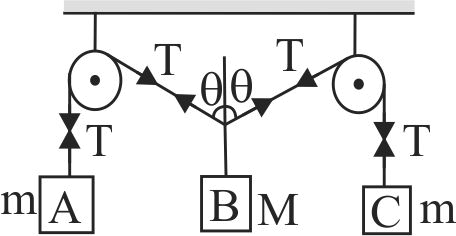
363308 A steel wire can withstand a load upto \(2940\;N\). A load of \(150\;kg\) is suspended from a rigid support. The maximum angle through which the wire can be displaced from the mean position, so that the wire does not break when the load passes through the position of equilibrium, is