363214 The maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius \(R\) and coefficient of static friction \(\mu \), is

363215 An object moves at a constant speed along a circular path in a horizontal plane with center at the origin. When the object is at \(x = + 2\,m\), its velocity is \( - 4\hat j\,m/s\). The object's velocity (\(v\)) and acceleration \((a)\) at \(x = - 2\,m\) will be

363216 A ring of mass \(m\) moves from point 1 to point 2 along a smooth rigid horizontal wire with a constant speed \(v\). The average force acting on the ring over the time of its motion from 1 to 2 is

363217 A block of mass 10 \(kg\) is in contact against the inner wall of a hollow cylindrical drum of radius 1 \(m\). The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : (\(g = 10\,m/{s^2}\))

363214 The maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius \(R\) and coefficient of static friction \(\mu \), is

363215 An object moves at a constant speed along a circular path in a horizontal plane with center at the origin. When the object is at \(x = + 2\,m\), its velocity is \( - 4\hat j\,m/s\). The object's velocity (\(v\)) and acceleration \((a)\) at \(x = - 2\,m\) will be

363216 A ring of mass \(m\) moves from point 1 to point 2 along a smooth rigid horizontal wire with a constant speed \(v\). The average force acting on the ring over the time of its motion from 1 to 2 is

363217 A block of mass 10 \(kg\) is in contact against the inner wall of a hollow cylindrical drum of radius 1 \(m\). The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : (\(g = 10\,m/{s^2}\))

363214 The maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius \(R\) and coefficient of static friction \(\mu \), is

363215 An object moves at a constant speed along a circular path in a horizontal plane with center at the origin. When the object is at \(x = + 2\,m\), its velocity is \( - 4\hat j\,m/s\). The object's velocity (\(v\)) and acceleration \((a)\) at \(x = - 2\,m\) will be

363216 A ring of mass \(m\) moves from point 1 to point 2 along a smooth rigid horizontal wire with a constant speed \(v\). The average force acting on the ring over the time of its motion from 1 to 2 is

363217 A block of mass 10 \(kg\) is in contact against the inner wall of a hollow cylindrical drum of radius 1 \(m\). The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : (\(g = 10\,m/{s^2}\))

363214 The maximum speed that can be achieved without skidding by a car on a circular unbanked road of radius \(R\) and coefficient of static friction \(\mu \), is

363215 An object moves at a constant speed along a circular path in a horizontal plane with center at the origin. When the object is at \(x = + 2\,m\), its velocity is \( - 4\hat j\,m/s\). The object's velocity (\(v\)) and acceleration \((a)\) at \(x = - 2\,m\) will be

363216 A ring of mass \(m\) moves from point 1 to point 2 along a smooth rigid horizontal wire with a constant speed \(v\). The average force acting on the ring over the time of its motion from 1 to 2 is

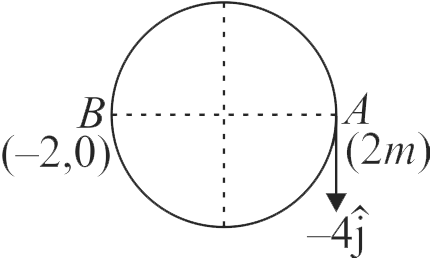
363217 A block of mass 10 \(kg\) is in contact against the inner wall of a hollow cylindrical drum of radius 1 \(m\). The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : (\(g = 10\,m/{s^2}\))