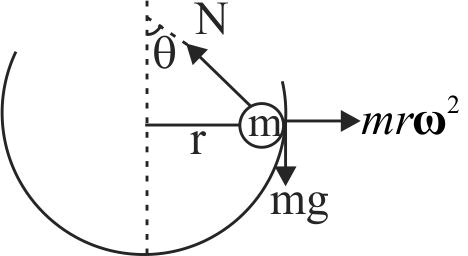
363218 A hemispherical bowl of radius \(R\) is rotated about its axis of symmetry which is kept vertical with angular velocity \(\omega \). A small block is kept in the bowl. It remains stationary relative to the bowl surface at a position where the radius makes an angle \(\theta \) with the vertical. The friction is absent. The value of \(\theta \) is :-
363221
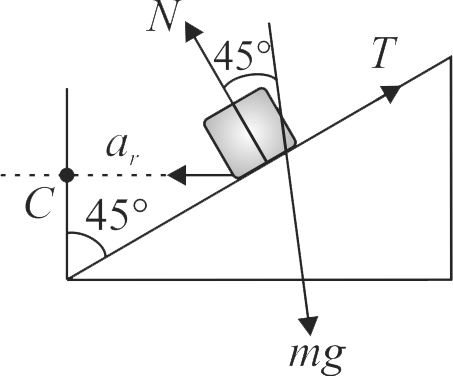
A small block of mass \(1\,kg\) is held by a light string rests on a smooth inclined plane which can turn about \({Z Z^{\prime}}\)-axis with an angular velocity \(2\,rad/s\) as shown in the figure. The block is at distance \({\dfrac{1}{\sqrt{2}} {~m}}\) from the point \({O}\). The tension in the string is \({(32)^{x} {~N}}\). Find the value of \({x}\) is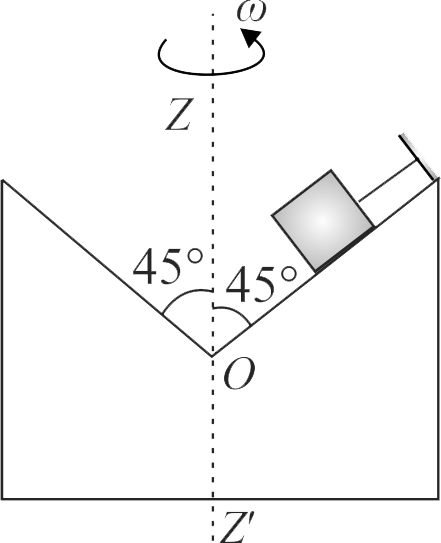
363222
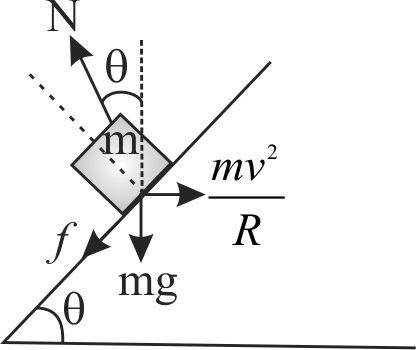
A person is driving a vehicle at uniform speed of \(5\,m{s^{ - 1}}\) on a level curved track of radius 5 \(m\). The coefficient of static friction between tyres and road is 0.1. Will the person slip while taking the turn with the same speed ? Take \(g = 10\,m{s^{ - 2}}\).
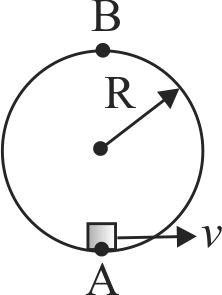
Choose the correct statement.
363218 A hemispherical bowl of radius \(R\) is rotated about its axis of symmetry which is kept vertical with angular velocity \(\omega \). A small block is kept in the bowl. It remains stationary relative to the bowl surface at a position where the radius makes an angle \(\theta \) with the vertical. The friction is absent. The value of \(\theta \) is :-
363221
A small block of mass \(1\,kg\) is held by a light string rests on a smooth inclined plane which can turn about \({Z Z^{\prime}}\)-axis with an angular velocity \(2\,rad/s\) as shown in the figure. The block is at distance \({\dfrac{1}{\sqrt{2}} {~m}}\) from the point \({O}\). The tension in the string is \({(32)^{x} {~N}}\). Find the value of \({x}\) is
363222
A person is driving a vehicle at uniform speed of \(5\,m{s^{ - 1}}\) on a level curved track of radius 5 \(m\). The coefficient of static friction between tyres and road is 0.1. Will the person slip while taking the turn with the same speed ? Take \(g = 10\,m{s^{ - 2}}\).
Choose the correct statement.
363218 A hemispherical bowl of radius \(R\) is rotated about its axis of symmetry which is kept vertical with angular velocity \(\omega \). A small block is kept in the bowl. It remains stationary relative to the bowl surface at a position where the radius makes an angle \(\theta \) with the vertical. The friction is absent. The value of \(\theta \) is :-
363221
A small block of mass \(1\,kg\) is held by a light string rests on a smooth inclined plane which can turn about \({Z Z^{\prime}}\)-axis with an angular velocity \(2\,rad/s\) as shown in the figure. The block is at distance \({\dfrac{1}{\sqrt{2}} {~m}}\) from the point \({O}\). The tension in the string is \({(32)^{x} {~N}}\). Find the value of \({x}\) is
363222
A person is driving a vehicle at uniform speed of \(5\,m{s^{ - 1}}\) on a level curved track of radius 5 \(m\). The coefficient of static friction between tyres and road is 0.1. Will the person slip while taking the turn with the same speed ? Take \(g = 10\,m{s^{ - 2}}\).
Choose the correct statement.
363218 A hemispherical bowl of radius \(R\) is rotated about its axis of symmetry which is kept vertical with angular velocity \(\omega \). A small block is kept in the bowl. It remains stationary relative to the bowl surface at a position where the radius makes an angle \(\theta \) with the vertical. The friction is absent. The value of \(\theta \) is :-
363221
A small block of mass \(1\,kg\) is held by a light string rests on a smooth inclined plane which can turn about \({Z Z^{\prime}}\)-axis with an angular velocity \(2\,rad/s\) as shown in the figure. The block is at distance \({\dfrac{1}{\sqrt{2}} {~m}}\) from the point \({O}\). The tension in the string is \({(32)^{x} {~N}}\). Find the value of \({x}\) is
363222
A person is driving a vehicle at uniform speed of \(5\,m{s^{ - 1}}\) on a level curved track of radius 5 \(m\). The coefficient of static friction between tyres and road is 0.1. Will the person slip while taking the turn with the same speed ? Take \(g = 10\,m{s^{ - 2}}\).
Choose the correct statement.
363218 A hemispherical bowl of radius \(R\) is rotated about its axis of symmetry which is kept vertical with angular velocity \(\omega \). A small block is kept in the bowl. It remains stationary relative to the bowl surface at a position where the radius makes an angle \(\theta \) with the vertical. The friction is absent. The value of \(\theta \) is :-
363221
A small block of mass \(1\,kg\) is held by a light string rests on a smooth inclined plane which can turn about \({Z Z^{\prime}}\)-axis with an angular velocity \(2\,rad/s\) as shown in the figure. The block is at distance \({\dfrac{1}{\sqrt{2}} {~m}}\) from the point \({O}\). The tension in the string is \({(32)^{x} {~N}}\). Find the value of \({x}\) is
363222
A person is driving a vehicle at uniform speed of \(5\,m{s^{ - 1}}\) on a level curved track of radius 5 \(m\). The coefficient of static friction between tyres and road is 0.1. Will the person slip while taking the turn with the same speed ? Take \(g = 10\,m{s^{ - 2}}\).
Choose the correct statement.