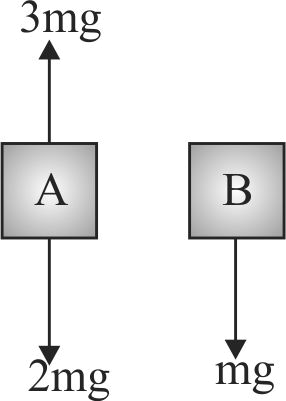
363100
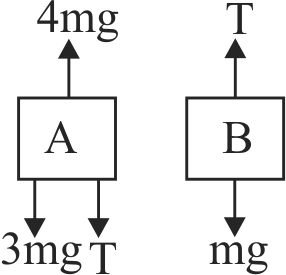
Two blocks \(A\) and \(B\) of masses 3 \(m\) and \(m\) respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively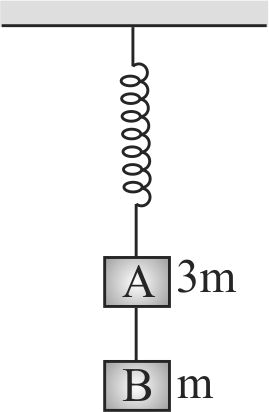
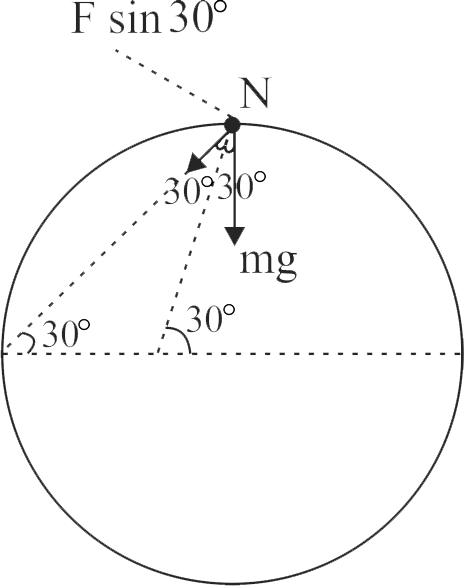
363102 A bead of mass \(m\) is attached to one end spring of natural length \(R\) and spring constant \(K = \frac{{(1 + \sqrt 3 )mg}}{R}\). The other end of the spring is fixed at a point \(A\) on a smooth vertical ring of radius \(R\). The normal reaction at \(B\) just after it is released to move is:
363103
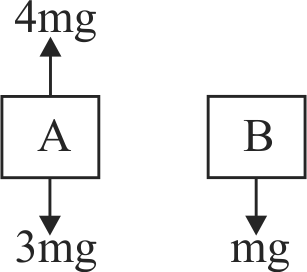
Two blocks \(A\) and \(B\) of masses 2 \(m\) and \(m\), respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively:
363100
Two blocks \(A\) and \(B\) of masses 3 \(m\) and \(m\) respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively
363102 A bead of mass \(m\) is attached to one end spring of natural length \(R\) and spring constant \(K = \frac{{(1 + \sqrt 3 )mg}}{R}\). The other end of the spring is fixed at a point \(A\) on a smooth vertical ring of radius \(R\). The normal reaction at \(B\) just after it is released to move is:
363103
Two blocks \(A\) and \(B\) of masses 2 \(m\) and \(m\), respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively:
363100
Two blocks \(A\) and \(B\) of masses 3 \(m\) and \(m\) respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively
363102 A bead of mass \(m\) is attached to one end spring of natural length \(R\) and spring constant \(K = \frac{{(1 + \sqrt 3 )mg}}{R}\). The other end of the spring is fixed at a point \(A\) on a smooth vertical ring of radius \(R\). The normal reaction at \(B\) just after it is released to move is:
363103
Two blocks \(A\) and \(B\) of masses 2 \(m\) and \(m\), respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively:
363100
Two blocks \(A\) and \(B\) of masses 3 \(m\) and \(m\) respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively
363102 A bead of mass \(m\) is attached to one end spring of natural length \(R\) and spring constant \(K = \frac{{(1 + \sqrt 3 )mg}}{R}\). The other end of the spring is fixed at a point \(A\) on a smooth vertical ring of radius \(R\). The normal reaction at \(B\) just after it is released to move is:
363103
Two blocks \(A\) and \(B\) of masses 2 \(m\) and \(m\), respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of \(A\) and \(B\) immediately after the string is cut, are respectively: