363096
Two masses of \(10\,kg\) and \(20\,kg\) are connected by a massless spring, as shown in the figure. A force of \(100\,N\) acts on the \(20\,kg\) mass at the instant when the \(10\,kg\) mass has an acceleration of \({6 {~m} / {s}^{2}}\) towards right, the acceleration of the \(20\,kg\) mass is
363098
A block of mass 3 \(kg\) is initially in equilibrium and is hanging by two identical springs \(A\) and \(B\) as shown in figure. If spring \(A\) is cut from lower point at \(t = 0\) then, find acceleration of block in \(m{s^{ - 2}}\) at \(t = 0\). (ignore rotational effect.)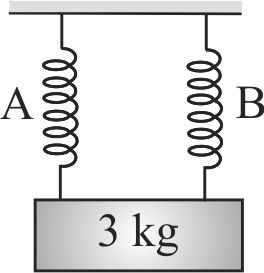
363099
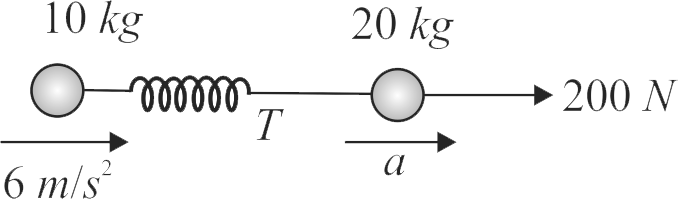
Two masses \(10\,kg\) and \(20\,kg\) respectively are connected by a massless spring as shown in figure. A force of \(200\,N\) acts on the \(20\;kg\) mass. At the instant shown is figure, the \(10\;kg\) mass has acceleration of \(12\;m/{s^2}.\) The value of acceleration of \(20\;kg\) mass is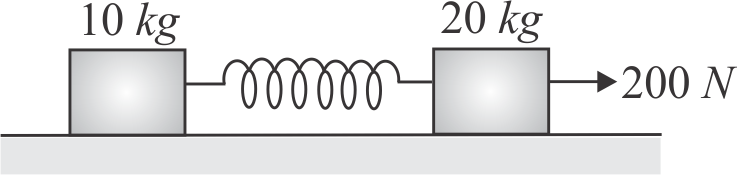
363096
Two masses of \(10\,kg\) and \(20\,kg\) are connected by a massless spring, as shown in the figure. A force of \(100\,N\) acts on the \(20\,kg\) mass at the instant when the \(10\,kg\) mass has an acceleration of \({6 {~m} / {s}^{2}}\) towards right, the acceleration of the \(20\,kg\) mass is
363098
A block of mass 3 \(kg\) is initially in equilibrium and is hanging by two identical springs \(A\) and \(B\) as shown in figure. If spring \(A\) is cut from lower point at \(t = 0\) then, find acceleration of block in \(m{s^{ - 2}}\) at \(t = 0\). (ignore rotational effect.)
363099
Two masses \(10\,kg\) and \(20\,kg\) respectively are connected by a massless spring as shown in figure. A force of \(200\,N\) acts on the \(20\;kg\) mass. At the instant shown is figure, the \(10\;kg\) mass has acceleration of \(12\;m/{s^2}.\) The value of acceleration of \(20\;kg\) mass is
363096
Two masses of \(10\,kg\) and \(20\,kg\) are connected by a massless spring, as shown in the figure. A force of \(100\,N\) acts on the \(20\,kg\) mass at the instant when the \(10\,kg\) mass has an acceleration of \({6 {~m} / {s}^{2}}\) towards right, the acceleration of the \(20\,kg\) mass is
363098
A block of mass 3 \(kg\) is initially in equilibrium and is hanging by two identical springs \(A\) and \(B\) as shown in figure. If spring \(A\) is cut from lower point at \(t = 0\) then, find acceleration of block in \(m{s^{ - 2}}\) at \(t = 0\). (ignore rotational effect.)
363099
Two masses \(10\,kg\) and \(20\,kg\) respectively are connected by a massless spring as shown in figure. A force of \(200\,N\) acts on the \(20\;kg\) mass. At the instant shown is figure, the \(10\;kg\) mass has acceleration of \(12\;m/{s^2}.\) The value of acceleration of \(20\;kg\) mass is
363096
Two masses of \(10\,kg\) and \(20\,kg\) are connected by a massless spring, as shown in the figure. A force of \(100\,N\) acts on the \(20\,kg\) mass at the instant when the \(10\,kg\) mass has an acceleration of \({6 {~m} / {s}^{2}}\) towards right, the acceleration of the \(20\,kg\) mass is
363098
A block of mass 3 \(kg\) is initially in equilibrium and is hanging by two identical springs \(A\) and \(B\) as shown in figure. If spring \(A\) is cut from lower point at \(t = 0\) then, find acceleration of block in \(m{s^{ - 2}}\) at \(t = 0\). (ignore rotational effect.)
363099
Two masses \(10\,kg\) and \(20\,kg\) respectively are connected by a massless spring as shown in figure. A force of \(200\,N\) acts on the \(20\;kg\) mass. At the instant shown is figure, the \(10\;kg\) mass has acceleration of \(12\;m/{s^2}.\) The value of acceleration of \(20\;kg\) mass is
363096
Two masses of \(10\,kg\) and \(20\,kg\) are connected by a massless spring, as shown in the figure. A force of \(100\,N\) acts on the \(20\,kg\) mass at the instant when the \(10\,kg\) mass has an acceleration of \({6 {~m} / {s}^{2}}\) towards right, the acceleration of the \(20\,kg\) mass is
363098
A block of mass 3 \(kg\) is initially in equilibrium and is hanging by two identical springs \(A\) and \(B\) as shown in figure. If spring \(A\) is cut from lower point at \(t = 0\) then, find acceleration of block in \(m{s^{ - 2}}\) at \(t = 0\). (ignore rotational effect.)
363099
Two masses \(10\,kg\) and \(20\,kg\) respectively are connected by a massless spring as shown in figure. A force of \(200\,N\) acts on the \(20\;kg\) mass. At the instant shown is figure, the \(10\;kg\) mass has acceleration of \(12\;m/{s^2}.\) The value of acceleration of \(20\;kg\) mass is

.png)
