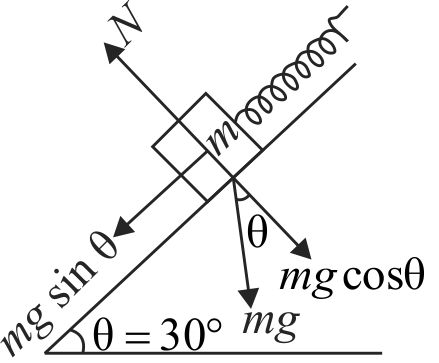
363091
In the figure, block \(A\) and \(B\) of masses \(2 m\) and \(m\) are connected with a string and system is hanged vertically with the help of a spring. Spring has negligible mass. Find out magnitude of acceleration of masses \(2 m\) and \(m\) just after the instant when the string of mass \(m\) is cut.png)
363092
Two blocks are connected by a spring. The combination is suspended, at rest, from a string attached to the ceiling, as shown in the figure. The string breaks suddenly. Immediately after the string breaks, what is the initial downward acceleration of the upper block of mass 2 \(m\)?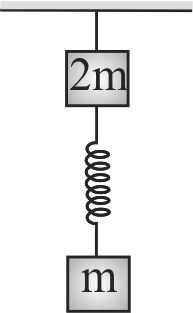
363094
Two masses of 10 \(kg\) and 20 \(kg\) respectively, are connected by a light spring as shown in the figure. A force of 200 \(N\) acts upon the 20 \(kg\) mass. At the instant shown, the 10 \(kg\) mass has acceleration of \(12\,m/{s^2}\). The acceleration of 20 \(kg\) mass is: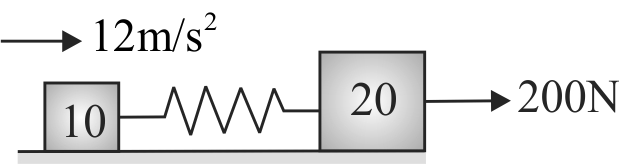
363091
In the figure, block \(A\) and \(B\) of masses \(2 m\) and \(m\) are connected with a string and system is hanged vertically with the help of a spring. Spring has negligible mass. Find out magnitude of acceleration of masses \(2 m\) and \(m\) just after the instant when the string of mass \(m\) is cut.png)
363092
Two blocks are connected by a spring. The combination is suspended, at rest, from a string attached to the ceiling, as shown in the figure. The string breaks suddenly. Immediately after the string breaks, what is the initial downward acceleration of the upper block of mass 2 \(m\)?
363094
Two masses of 10 \(kg\) and 20 \(kg\) respectively, are connected by a light spring as shown in the figure. A force of 200 \(N\) acts upon the 20 \(kg\) mass. At the instant shown, the 10 \(kg\) mass has acceleration of \(12\,m/{s^2}\). The acceleration of 20 \(kg\) mass is:
363091
In the figure, block \(A\) and \(B\) of masses \(2 m\) and \(m\) are connected with a string and system is hanged vertically with the help of a spring. Spring has negligible mass. Find out magnitude of acceleration of masses \(2 m\) and \(m\) just after the instant when the string of mass \(m\) is cut.png)
363092
Two blocks are connected by a spring. The combination is suspended, at rest, from a string attached to the ceiling, as shown in the figure. The string breaks suddenly. Immediately after the string breaks, what is the initial downward acceleration of the upper block of mass 2 \(m\)?
363094
Two masses of 10 \(kg\) and 20 \(kg\) respectively, are connected by a light spring as shown in the figure. A force of 200 \(N\) acts upon the 20 \(kg\) mass. At the instant shown, the 10 \(kg\) mass has acceleration of \(12\,m/{s^2}\). The acceleration of 20 \(kg\) mass is:
363091
In the figure, block \(A\) and \(B\) of masses \(2 m\) and \(m\) are connected with a string and system is hanged vertically with the help of a spring. Spring has negligible mass. Find out magnitude of acceleration of masses \(2 m\) and \(m\) just after the instant when the string of mass \(m\) is cut.png)
363092
Two blocks are connected by a spring. The combination is suspended, at rest, from a string attached to the ceiling, as shown in the figure. The string breaks suddenly. Immediately after the string breaks, what is the initial downward acceleration of the upper block of mass 2 \(m\)?
363094
Two masses of 10 \(kg\) and 20 \(kg\) respectively, are connected by a light spring as shown in the figure. A force of 200 \(N\) acts upon the 20 \(kg\) mass. At the instant shown, the 10 \(kg\) mass has acceleration of \(12\,m/{s^2}\). The acceleration of 20 \(kg\) mass is:
.png)