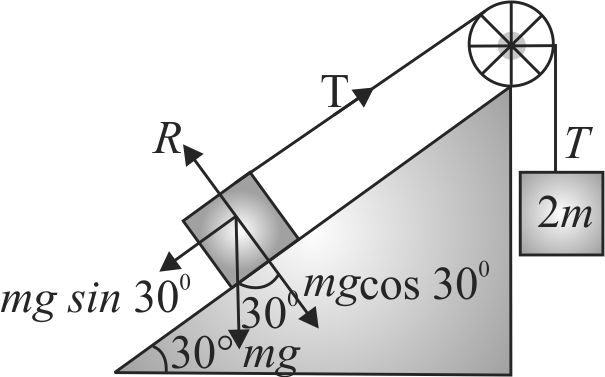
363087 Two blocks of masses \(m\) and 2 \(m\) are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass \(m\) is placed on a smooth inclined plane of inclination \(30^\circ \) and 2 \(m\) hangs vertically. If the system is released, the blocks move with an acceleration equal to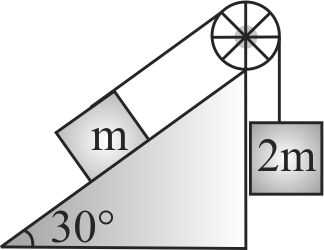

363088 An insect of mass \(m\) crawls along the hanging thread with an acceleration \(a = \frac{g}{2}\). The reaction offered by ground on the block of mass 2 \(m\) is:

363089 A light string passing over a smooth light pulley connects two blocks of masses \(m_{1}\) and \(m_{2}\) (where \(m_{2}>m_{1}\) ). If the acceleration of the system is \(\dfrac{g}{\sqrt{2}}\), then the ratio of the masses \(\dfrac{m_{1}}{m_{2}}\) is

363090 If the system shown in figure is released from rest then acceleration of 2 \(kg\) block is (take \(g = 10\,m/{s^2}\) and the pulleys are very light)

363087 Two blocks of masses \(m\) and 2 \(m\) are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass \(m\) is placed on a smooth inclined plane of inclination \(30^\circ \) and 2 \(m\) hangs vertically. If the system is released, the blocks move with an acceleration equal to

363088 An insect of mass \(m\) crawls along the hanging thread with an acceleration \(a = \frac{g}{2}\). The reaction offered by ground on the block of mass 2 \(m\) is:

363089 A light string passing over a smooth light pulley connects two blocks of masses \(m_{1}\) and \(m_{2}\) (where \(m_{2}>m_{1}\) ). If the acceleration of the system is \(\dfrac{g}{\sqrt{2}}\), then the ratio of the masses \(\dfrac{m_{1}}{m_{2}}\) is

363090 If the system shown in figure is released from rest then acceleration of 2 \(kg\) block is (take \(g = 10\,m/{s^2}\) and the pulleys are very light)

363087 Two blocks of masses \(m\) and 2 \(m\) are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass \(m\) is placed on a smooth inclined plane of inclination \(30^\circ \) and 2 \(m\) hangs vertically. If the system is released, the blocks move with an acceleration equal to

363088 An insect of mass \(m\) crawls along the hanging thread with an acceleration \(a = \frac{g}{2}\). The reaction offered by ground on the block of mass 2 \(m\) is:

363089 A light string passing over a smooth light pulley connects two blocks of masses \(m_{1}\) and \(m_{2}\) (where \(m_{2}>m_{1}\) ). If the acceleration of the system is \(\dfrac{g}{\sqrt{2}}\), then the ratio of the masses \(\dfrac{m_{1}}{m_{2}}\) is

363090 If the system shown in figure is released from rest then acceleration of 2 \(kg\) block is (take \(g = 10\,m/{s^2}\) and the pulleys are very light)

363087 Two blocks of masses \(m\) and 2 \(m\) are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass \(m\) is placed on a smooth inclined plane of inclination \(30^\circ \) and 2 \(m\) hangs vertically. If the system is released, the blocks move with an acceleration equal to

363088 An insect of mass \(m\) crawls along the hanging thread with an acceleration \(a = \frac{g}{2}\). The reaction offered by ground on the block of mass 2 \(m\) is:

363089 A light string passing over a smooth light pulley connects two blocks of masses \(m_{1}\) and \(m_{2}\) (where \(m_{2}>m_{1}\) ). If the acceleration of the system is \(\dfrac{g}{\sqrt{2}}\), then the ratio of the masses \(\dfrac{m_{1}}{m_{2}}\) is

363090 If the system shown in figure is released from rest then acceleration of 2 \(kg\) block is (take \(g = 10\,m/{s^2}\) and the pulleys are very light)