362591
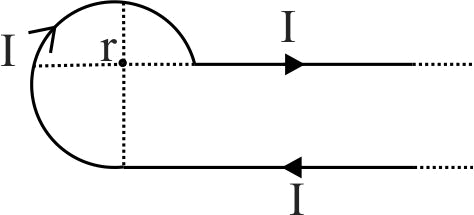
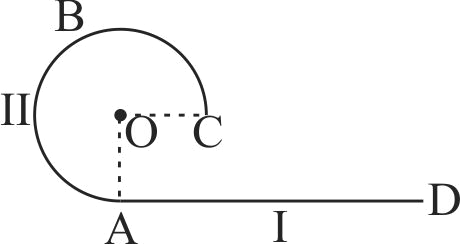
Circular loop of a wire and a long straight wire carry currents \(I_{c}\) and \(I_{e}\), respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation \(H\) is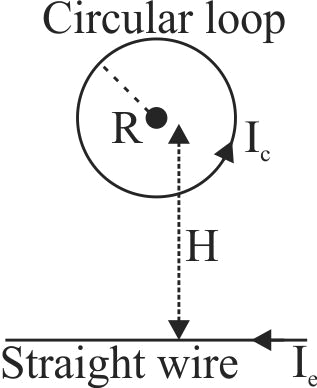
362592
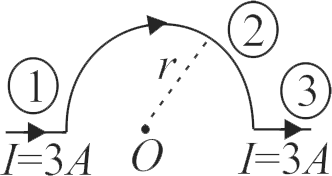
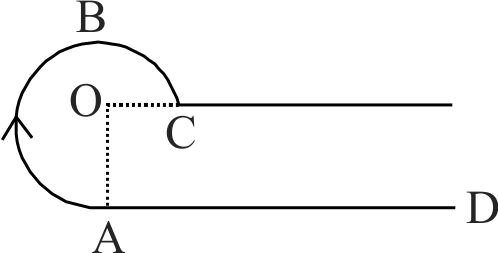
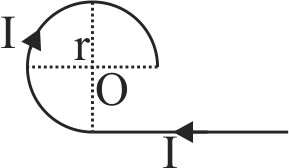
As shown in the figure, a long straight conductor with semi-circular arc of radius \(\dfrac{\pi}{10} m\) is carrying current \(I = 3\;A\). The magnitude of the magnetic field at the center \(O\) of the arc is
(The permeability of the vacuum \(=4 \pi \times 10^{-7} N A^{-2}\))
362591
Circular loop of a wire and a long straight wire carry currents \(I_{c}\) and \(I_{e}\), respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation \(H\) is
362592
As shown in the figure, a long straight conductor with semi-circular arc of radius \(\dfrac{\pi}{10} m\) is carrying current \(I = 3\;A\). The magnitude of the magnetic field at the center \(O\) of the arc is
(The permeability of the vacuum \(=4 \pi \times 10^{-7} N A^{-2}\))
362591
Circular loop of a wire and a long straight wire carry currents \(I_{c}\) and \(I_{e}\), respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation \(H\) is
362592
As shown in the figure, a long straight conductor with semi-circular arc of radius \(\dfrac{\pi}{10} m\) is carrying current \(I = 3\;A\). The magnitude of the magnetic field at the center \(O\) of the arc is
(The permeability of the vacuum \(=4 \pi \times 10^{-7} N A^{-2}\))
362591
Circular loop of a wire and a long straight wire carry currents \(I_{c}\) and \(I_{e}\), respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation \(H\) is
362592
As shown in the figure, a long straight conductor with semi-circular arc of radius \(\dfrac{\pi}{10} m\) is carrying current \(I = 3\;A\). The magnitude of the magnetic field at the center \(O\) of the arc is
(The permeability of the vacuum \(=4 \pi \times 10^{-7} N A^{-2}\))
362591
Circular loop of a wire and a long straight wire carry currents \(I_{c}\) and \(I_{e}\), respectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation \(H\) is
362592
As shown in the figure, a long straight conductor with semi-circular arc of radius \(\dfrac{\pi}{10} m\) is carrying current \(I = 3\;A\). The magnitude of the magnetic field at the center \(O\) of the arc is
(The permeability of the vacuum \(=4 \pi \times 10^{-7} N A^{-2}\))