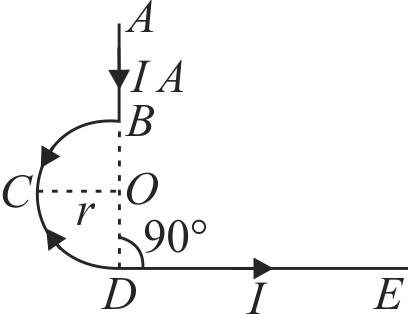
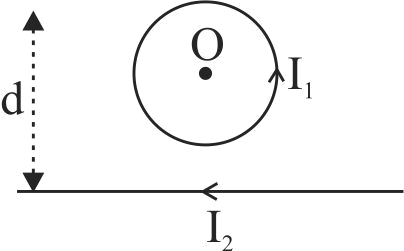
362597 A circular coil of radius \(R\) is carrying a current \(I_{1}\) in anti clock wise sense. A long straight wire is carrying current \(I_{2}\) in the negative direction of X - axis. Both are placed in the same plane and the distance between centre of coil and straight wire is \(d\). The magnetic field at the centre of coil will be zero for the value of \(d\) equal to
362598
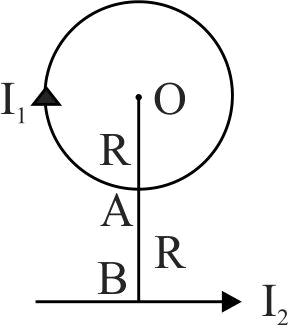
In the diagram, \(I_{1}, I_{2}\) are the strength of the currents in the loop and straight conductors respectively.\(OA = OB = R\). The net magnetic field at the centre \(O\) is zero.Then the ratio of the currents in the loop and the straight conductors is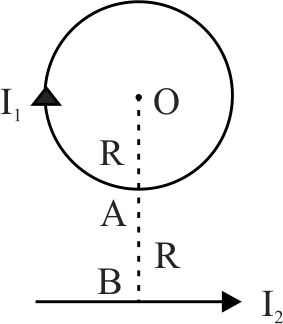
362599
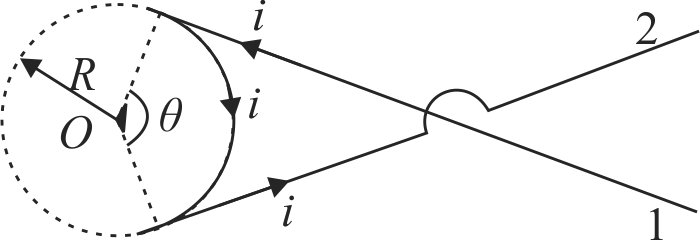
A wire carrying current \({i}\) has the configuration shown in figure. Two semi-infinite straight sections, each tangent to the same circle, are connected by a circular arc, of angle \({\theta}\), along the circumference of the circle, with all sections lying in the same plane. What must \({\theta}\) be in order for \({B}\) to be zero at the center of circle?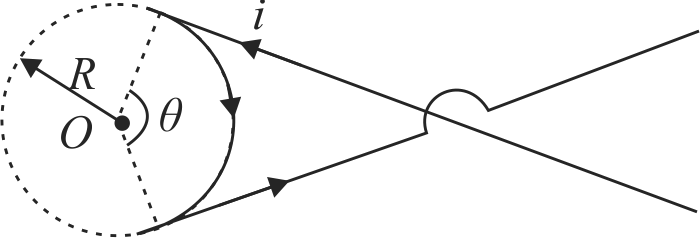
362597 A circular coil of radius \(R\) is carrying a current \(I_{1}\) in anti clock wise sense. A long straight wire is carrying current \(I_{2}\) in the negative direction of X - axis. Both are placed in the same plane and the distance between centre of coil and straight wire is \(d\). The magnetic field at the centre of coil will be zero for the value of \(d\) equal to
362598
In the diagram, \(I_{1}, I_{2}\) are the strength of the currents in the loop and straight conductors respectively.\(OA = OB = R\). The net magnetic field at the centre \(O\) is zero.Then the ratio of the currents in the loop and the straight conductors is
362599
A wire carrying current \({i}\) has the configuration shown in figure. Two semi-infinite straight sections, each tangent to the same circle, are connected by a circular arc, of angle \({\theta}\), along the circumference of the circle, with all sections lying in the same plane. What must \({\theta}\) be in order for \({B}\) to be zero at the center of circle?
362597 A circular coil of radius \(R\) is carrying a current \(I_{1}\) in anti clock wise sense. A long straight wire is carrying current \(I_{2}\) in the negative direction of X - axis. Both are placed in the same plane and the distance between centre of coil and straight wire is \(d\). The magnetic field at the centre of coil will be zero for the value of \(d\) equal to
362598
In the diagram, \(I_{1}, I_{2}\) are the strength of the currents in the loop and straight conductors respectively.\(OA = OB = R\). The net magnetic field at the centre \(O\) is zero.Then the ratio of the currents in the loop and the straight conductors is
362599
A wire carrying current \({i}\) has the configuration shown in figure. Two semi-infinite straight sections, each tangent to the same circle, are connected by a circular arc, of angle \({\theta}\), along the circumference of the circle, with all sections lying in the same plane. What must \({\theta}\) be in order for \({B}\) to be zero at the center of circle?
362597 A circular coil of radius \(R\) is carrying a current \(I_{1}\) in anti clock wise sense. A long straight wire is carrying current \(I_{2}\) in the negative direction of X - axis. Both are placed in the same plane and the distance between centre of coil and straight wire is \(d\). The magnetic field at the centre of coil will be zero for the value of \(d\) equal to
362598
In the diagram, \(I_{1}, I_{2}\) are the strength of the currents in the loop and straight conductors respectively.\(OA = OB = R\). The net magnetic field at the centre \(O\) is zero.Then the ratio of the currents in the loop and the straight conductors is
362599
A wire carrying current \({i}\) has the configuration shown in figure. Two semi-infinite straight sections, each tangent to the same circle, are connected by a circular arc, of angle \({\theta}\), along the circumference of the circle, with all sections lying in the same plane. What must \({\theta}\) be in order for \({B}\) to be zero at the center of circle?