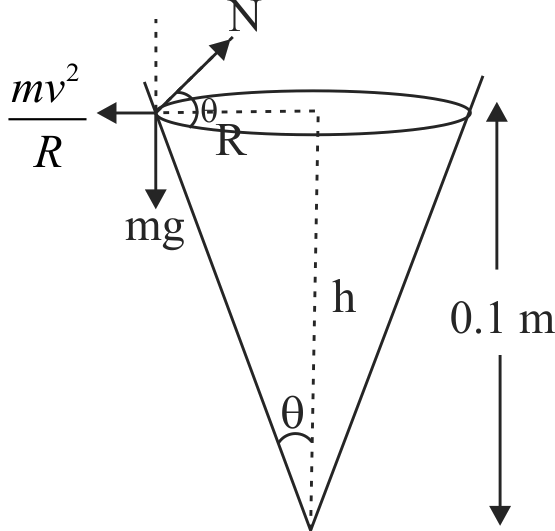
Explanation:
Forces acting on the ball are shown in the figure.
Using \(\frac{{m{v^2}}}{R} = N\cos \theta \,\,{\rm{and}}\,mg = N\sin \theta \)
we get \(\tan \theta = \frac{{gR}}{{{v^2}}}\)
or \(\frac{R}{h} = \frac{{gR}}{{{v^2}}}{\rm{i}}{\rm{.e}}{\rm{.,}}\,\,v = \sqrt {gh} \)
\( \Rightarrow \,\,\,\,v = \sqrt {10 \times 0.1} = 1\,m{s^{ - 1}}\)