361883 Two racing cars of masses \({m_1}\) and \({m_2}\) are moving in circles of radii \({r_1}\) and \({r_2}\) respectively. Their speeds are such that each makes a complete circle in the same duration of time \(t\). The ratio of the angular speed of the first to the second car is

361884 A pont \(P\) moves in counterclockwise direction on a circular path as shown in figure. The movement of \(P\) is such that it sweeps out a length \(S=t^{3}+8\), where \(S\) in metre and \(t\) is in seconds. The radius of the path is \(60 \mathrm{~m}\). The acceleration of \(P\) when \(t=4 s\) is near by: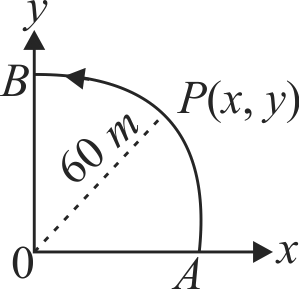

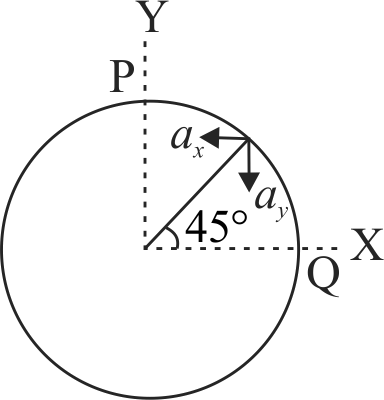
361885 A particle moves in a circle of radius 4 \(m\) clockwise at constant speed of \(2\,m\,{s^{ - 1}}.\) If \(\widehat x\) and \(\widehat y\) are unit vectors along \(x\) and \(y\) axis, respectively, the acceleration of the particle at the instant half way between \(PQ\) is given by

361886 A ball moves along an uneven horizontal road with fixed speed at all points on the road. The normal reaction of the road on the body at two different points \(A\) and \(B\) is

361883 Two racing cars of masses \({m_1}\) and \({m_2}\) are moving in circles of radii \({r_1}\) and \({r_2}\) respectively. Their speeds are such that each makes a complete circle in the same duration of time \(t\). The ratio of the angular speed of the first to the second car is

361884 A pont \(P\) moves in counterclockwise direction on a circular path as shown in figure. The movement of \(P\) is such that it sweeps out a length \(S=t^{3}+8\), where \(S\) in metre and \(t\) is in seconds. The radius of the path is \(60 \mathrm{~m}\). The acceleration of \(P\) when \(t=4 s\) is near by:

361885 A particle moves in a circle of radius 4 \(m\) clockwise at constant speed of \(2\,m\,{s^{ - 1}}.\) If \(\widehat x\) and \(\widehat y\) are unit vectors along \(x\) and \(y\) axis, respectively, the acceleration of the particle at the instant half way between \(PQ\) is given by

361886 A ball moves along an uneven horizontal road with fixed speed at all points on the road. The normal reaction of the road on the body at two different points \(A\) and \(B\) is

361883 Two racing cars of masses \({m_1}\) and \({m_2}\) are moving in circles of radii \({r_1}\) and \({r_2}\) respectively. Their speeds are such that each makes a complete circle in the same duration of time \(t\). The ratio of the angular speed of the first to the second car is

361884 A pont \(P\) moves in counterclockwise direction on a circular path as shown in figure. The movement of \(P\) is such that it sweeps out a length \(S=t^{3}+8\), where \(S\) in metre and \(t\) is in seconds. The radius of the path is \(60 \mathrm{~m}\). The acceleration of \(P\) when \(t=4 s\) is near by:

361885 A particle moves in a circle of radius 4 \(m\) clockwise at constant speed of \(2\,m\,{s^{ - 1}}.\) If \(\widehat x\) and \(\widehat y\) are unit vectors along \(x\) and \(y\) axis, respectively, the acceleration of the particle at the instant half way between \(PQ\) is given by

361886 A ball moves along an uneven horizontal road with fixed speed at all points on the road. The normal reaction of the road on the body at two different points \(A\) and \(B\) is

361883 Two racing cars of masses \({m_1}\) and \({m_2}\) are moving in circles of radii \({r_1}\) and \({r_2}\) respectively. Their speeds are such that each makes a complete circle in the same duration of time \(t\). The ratio of the angular speed of the first to the second car is

361884 A pont \(P\) moves in counterclockwise direction on a circular path as shown in figure. The movement of \(P\) is such that it sweeps out a length \(S=t^{3}+8\), where \(S\) in metre and \(t\) is in seconds. The radius of the path is \(60 \mathrm{~m}\). The acceleration of \(P\) when \(t=4 s\) is near by:

361885 A particle moves in a circle of radius 4 \(m\) clockwise at constant speed of \(2\,m\,{s^{ - 1}}.\) If \(\widehat x\) and \(\widehat y\) are unit vectors along \(x\) and \(y\) axis, respectively, the acceleration of the particle at the instant half way between \(PQ\) is given by

361886 A ball moves along an uneven horizontal road with fixed speed at all points on the road. The normal reaction of the road on the body at two different points \(A\) and \(B\) is