361835 A particle moving with a constant speed of \({9 {~km} / {h}}\) on a circle reaches from end \({A}\) to the diametrically opposite end \({B}\) in time \({2 s}\). The average acceleration from \({A}\) to \({B}\) is

361836 A particle is moving in a circle of radius \(R\) with constant speed \(v\), if radius is doubled then its centripetal force to keep the same speed should be

361837 A particle is moving with constant speed \({v}\) in \({x-y}\) plane, as shown in the figure. The magnitude of its angular velocity about point \({O}\) is

361838 The angle turned by a body undergoing circular motion depends on time as \(\theta = {\theta _0} + {\theta _1}t + {\theta _2}{t^2}.\) Then the angular acceleration of the body is

361839 A point \(P\) moves in counter-clockwise direction on a circular path as shown in the figure. The movement of \('P'\) is such that it sweeps out a length \(s=t^{3}+5\), where \(s\) is in metres and \(t\) is in seconds. The radius of the path is \(27\;m.\) The acceleration of ' \(P\) ' when \(t = 3\;s\) is
(Take \(\sqrt{13}=3.6\) )

361835 A particle moving with a constant speed of \({9 {~km} / {h}}\) on a circle reaches from end \({A}\) to the diametrically opposite end \({B}\) in time \({2 s}\). The average acceleration from \({A}\) to \({B}\) is

361836 A particle is moving in a circle of radius \(R\) with constant speed \(v\), if radius is doubled then its centripetal force to keep the same speed should be

361837 A particle is moving with constant speed \({v}\) in \({x-y}\) plane, as shown in the figure. The magnitude of its angular velocity about point \({O}\) is

361838 The angle turned by a body undergoing circular motion depends on time as \(\theta = {\theta _0} + {\theta _1}t + {\theta _2}{t^2}.\) Then the angular acceleration of the body is

361839 A point \(P\) moves in counter-clockwise direction on a circular path as shown in the figure. The movement of \('P'\) is such that it sweeps out a length \(s=t^{3}+5\), where \(s\) is in metres and \(t\) is in seconds. The radius of the path is \(27\;m.\) The acceleration of ' \(P\) ' when \(t = 3\;s\) is
(Take \(\sqrt{13}=3.6\) )

361835 A particle moving with a constant speed of \({9 {~km} / {h}}\) on a circle reaches from end \({A}\) to the diametrically opposite end \({B}\) in time \({2 s}\). The average acceleration from \({A}\) to \({B}\) is

361836 A particle is moving in a circle of radius \(R\) with constant speed \(v\), if radius is doubled then its centripetal force to keep the same speed should be

361837 A particle is moving with constant speed \({v}\) in \({x-y}\) plane, as shown in the figure. The magnitude of its angular velocity about point \({O}\) is

361838 The angle turned by a body undergoing circular motion depends on time as \(\theta = {\theta _0} + {\theta _1}t + {\theta _2}{t^2}.\) Then the angular acceleration of the body is

361839 A point \(P\) moves in counter-clockwise direction on a circular path as shown in the figure. The movement of \('P'\) is such that it sweeps out a length \(s=t^{3}+5\), where \(s\) is in metres and \(t\) is in seconds. The radius of the path is \(27\;m.\) The acceleration of ' \(P\) ' when \(t = 3\;s\) is
(Take \(\sqrt{13}=3.6\) )

361835 A particle moving with a constant speed of \({9 {~km} / {h}}\) on a circle reaches from end \({A}\) to the diametrically opposite end \({B}\) in time \({2 s}\). The average acceleration from \({A}\) to \({B}\) is

361836 A particle is moving in a circle of radius \(R\) with constant speed \(v\), if radius is doubled then its centripetal force to keep the same speed should be

361837 A particle is moving with constant speed \({v}\) in \({x-y}\) plane, as shown in the figure. The magnitude of its angular velocity about point \({O}\) is

361838 The angle turned by a body undergoing circular motion depends on time as \(\theta = {\theta _0} + {\theta _1}t + {\theta _2}{t^2}.\) Then the angular acceleration of the body is

361839 A point \(P\) moves in counter-clockwise direction on a circular path as shown in the figure. The movement of \('P'\) is such that it sweeps out a length \(s=t^{3}+5\), where \(s\) is in metres and \(t\) is in seconds. The radius of the path is \(27\;m.\) The acceleration of ' \(P\) ' when \(t = 3\;s\) is
(Take \(\sqrt{13}=3.6\) )

361835 A particle moving with a constant speed of \({9 {~km} / {h}}\) on a circle reaches from end \({A}\) to the diametrically opposite end \({B}\) in time \({2 s}\). The average acceleration from \({A}\) to \({B}\) is

361836 A particle is moving in a circle of radius \(R\) with constant speed \(v\), if radius is doubled then its centripetal force to keep the same speed should be

361837 A particle is moving with constant speed \({v}\) in \({x-y}\) plane, as shown in the figure. The magnitude of its angular velocity about point \({O}\) is

361838 The angle turned by a body undergoing circular motion depends on time as \(\theta = {\theta _0} + {\theta _1}t + {\theta _2}{t^2}.\) Then the angular acceleration of the body is

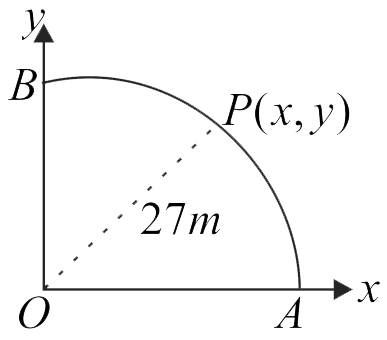
361839 A point \(P\) moves in counter-clockwise direction on a circular path as shown in the figure. The movement of \('P'\) is such that it sweeps out a length \(s=t^{3}+5\), where \(s\) is in metres and \(t\) is in seconds. The radius of the path is \(27\;m.\) The acceleration of ' \(P\) ' when \(t = 3\;s\) is
(Take \(\sqrt{13}=3.6\) )