369797 A copper wire of length \(1.0\;m\) and a steel wire of length \(0.5\;m\) having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by \(1 \mathrm{~mm}\). If the Young's modulii of copper and steel are respectively
\(1.0 \times {10^{11}}N{m^{ - 2}}\,{\text{and}}\,2.0 \times {10^{11}}N{m^{ - 2}}\), the total extension of the composite wire is:

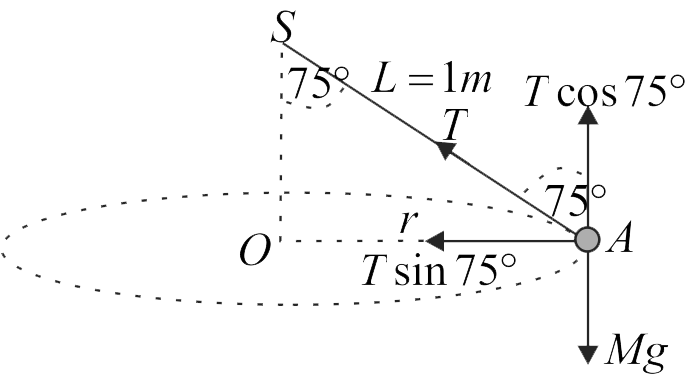
369798 A stone of \(0.5\;kg\) mass is attached to one end of a metre long aluminium wire of \(1\;mm\) diameter and is suspended vertically. The stone is now rotated in a horizontal plane at a rate, such that the wire makes an angle of \(75^{\circ}\) with the vertical. Find the increase in length of the wire. (Take Young's modulus of aluminium \( = 7 \times {10^{10}}N{m^{ - 2}},\sin 75^\circ \)\( = 0.97,\cos 75^\circ = 0.26,\)\(\pi = 3.14,g = 10\;m{\rm{/}}{s^2}\)

369799 A rod of length \(1\;\,m\) is connected to a ceiling and the lower end is connected to a load \(20\;\,N\). The extension produced in the rod is \({10^{ - 4}}\;\,m\). If the cross-sectional area of the wire is \({10^{ - 6}}\;\,{m^2}\), calculate the Young's modulus of the material of the wire.

369800 A fixed volume of iron is drawn into a wire of length \(l\). The extension produced in this wire by a constant force \(F\) is proportional to -

369797 A copper wire of length \(1.0\;m\) and a steel wire of length \(0.5\;m\) having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by \(1 \mathrm{~mm}\). If the Young's modulii of copper and steel are respectively
\(1.0 \times {10^{11}}N{m^{ - 2}}\,{\text{and}}\,2.0 \times {10^{11}}N{m^{ - 2}}\), the total extension of the composite wire is:

369798 A stone of \(0.5\;kg\) mass is attached to one end of a metre long aluminium wire of \(1\;mm\) diameter and is suspended vertically. The stone is now rotated in a horizontal plane at a rate, such that the wire makes an angle of \(75^{\circ}\) with the vertical. Find the increase in length of the wire. (Take Young's modulus of aluminium \( = 7 \times {10^{10}}N{m^{ - 2}},\sin 75^\circ \)\( = 0.97,\cos 75^\circ = 0.26,\)\(\pi = 3.14,g = 10\;m{\rm{/}}{s^2}\)

369799 A rod of length \(1\;\,m\) is connected to a ceiling and the lower end is connected to a load \(20\;\,N\). The extension produced in the rod is \({10^{ - 4}}\;\,m\). If the cross-sectional area of the wire is \({10^{ - 6}}\;\,{m^2}\), calculate the Young's modulus of the material of the wire.

369800 A fixed volume of iron is drawn into a wire of length \(l\). The extension produced in this wire by a constant force \(F\) is proportional to -

369797 A copper wire of length \(1.0\;m\) and a steel wire of length \(0.5\;m\) having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by \(1 \mathrm{~mm}\). If the Young's modulii of copper and steel are respectively
\(1.0 \times {10^{11}}N{m^{ - 2}}\,{\text{and}}\,2.0 \times {10^{11}}N{m^{ - 2}}\), the total extension of the composite wire is:

369798 A stone of \(0.5\;kg\) mass is attached to one end of a metre long aluminium wire of \(1\;mm\) diameter and is suspended vertically. The stone is now rotated in a horizontal plane at a rate, such that the wire makes an angle of \(75^{\circ}\) with the vertical. Find the increase in length of the wire. (Take Young's modulus of aluminium \( = 7 \times {10^{10}}N{m^{ - 2}},\sin 75^\circ \)\( = 0.97,\cos 75^\circ = 0.26,\)\(\pi = 3.14,g = 10\;m{\rm{/}}{s^2}\)

369799 A rod of length \(1\;\,m\) is connected to a ceiling and the lower end is connected to a load \(20\;\,N\). The extension produced in the rod is \({10^{ - 4}}\;\,m\). If the cross-sectional area of the wire is \({10^{ - 6}}\;\,{m^2}\), calculate the Young's modulus of the material of the wire.

369800 A fixed volume of iron is drawn into a wire of length \(l\). The extension produced in this wire by a constant force \(F\) is proportional to -

369797 A copper wire of length \(1.0\;m\) and a steel wire of length \(0.5\;m\) having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by \(1 \mathrm{~mm}\). If the Young's modulii of copper and steel are respectively
\(1.0 \times {10^{11}}N{m^{ - 2}}\,{\text{and}}\,2.0 \times {10^{11}}N{m^{ - 2}}\), the total extension of the composite wire is:

369798 A stone of \(0.5\;kg\) mass is attached to one end of a metre long aluminium wire of \(1\;mm\) diameter and is suspended vertically. The stone is now rotated in a horizontal plane at a rate, such that the wire makes an angle of \(75^{\circ}\) with the vertical. Find the increase in length of the wire. (Take Young's modulus of aluminium \( = 7 \times {10^{10}}N{m^{ - 2}},\sin 75^\circ \)\( = 0.97,\cos 75^\circ = 0.26,\)\(\pi = 3.14,g = 10\;m{\rm{/}}{s^2}\)

369799 A rod of length \(1\;\,m\) is connected to a ceiling and the lower end is connected to a load \(20\;\,N\). The extension produced in the rod is \({10^{ - 4}}\;\,m\). If the cross-sectional area of the wire is \({10^{ - 6}}\;\,{m^2}\), calculate the Young's modulus of the material of the wire.

369800 A fixed volume of iron is drawn into a wire of length \(l\). The extension produced in this wire by a constant force \(F\) is proportional to -