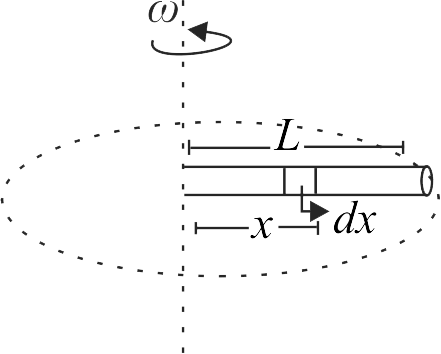
369788 A uniform rod of length \(L\) and density \(\rho\) is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is \(\omega\). If increase in the length is found to be \(\dfrac{\rho \omega^{2} L^{n}}{n Y}\) where, \(Y\) is Young's modulus of rod, determine value of \(n\).
369790
The graph shows the extension of a wire of length \(1\,m\) suspended from the top of a roof at one end and with a load \({W}\) connected to the other end. If the cross sectional area of the wire is \({1 {~mm}^{2}}\), then the Young's modulus of the material of the wire is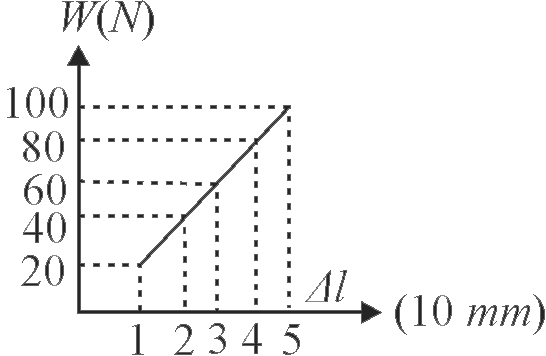
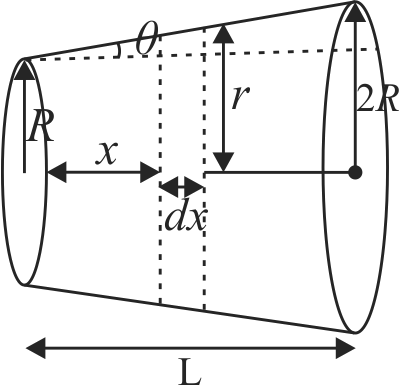
369792 A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values \(R\) and \(3 R\), respectively, The upper end of the wire is fixed to a rigid support and a mass \(M\) is suspended from its lower end. The equilibrium extended length, of this wire, would equal
369788 A uniform rod of length \(L\) and density \(\rho\) is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is \(\omega\). If increase in the length is found to be \(\dfrac{\rho \omega^{2} L^{n}}{n Y}\) where, \(Y\) is Young's modulus of rod, determine value of \(n\).
369790
The graph shows the extension of a wire of length \(1\,m\) suspended from the top of a roof at one end and with a load \({W}\) connected to the other end. If the cross sectional area of the wire is \({1 {~mm}^{2}}\), then the Young's modulus of the material of the wire is
369792 A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values \(R\) and \(3 R\), respectively, The upper end of the wire is fixed to a rigid support and a mass \(M\) is suspended from its lower end. The equilibrium extended length, of this wire, would equal
369788 A uniform rod of length \(L\) and density \(\rho\) is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is \(\omega\). If increase in the length is found to be \(\dfrac{\rho \omega^{2} L^{n}}{n Y}\) where, \(Y\) is Young's modulus of rod, determine value of \(n\).
369790
The graph shows the extension of a wire of length \(1\,m\) suspended from the top of a roof at one end and with a load \({W}\) connected to the other end. If the cross sectional area of the wire is \({1 {~mm}^{2}}\), then the Young's modulus of the material of the wire is
369792 A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values \(R\) and \(3 R\), respectively, The upper end of the wire is fixed to a rigid support and a mass \(M\) is suspended from its lower end. The equilibrium extended length, of this wire, would equal
369788 A uniform rod of length \(L\) and density \(\rho\) is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is \(\omega\). If increase in the length is found to be \(\dfrac{\rho \omega^{2} L^{n}}{n Y}\) where, \(Y\) is Young's modulus of rod, determine value of \(n\).
369790
The graph shows the extension of a wire of length \(1\,m\) suspended from the top of a roof at one end and with a load \({W}\) connected to the other end. If the cross sectional area of the wire is \({1 {~mm}^{2}}\), then the Young's modulus of the material of the wire is
369792 A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values \(R\) and \(3 R\), respectively, The upper end of the wire is fixed to a rigid support and a mass \(M\) is suspended from its lower end. The equilibrium extended length, of this wire, would equal
369788 A uniform rod of length \(L\) and density \(\rho\) is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is \(\omega\). If increase in the length is found to be \(\dfrac{\rho \omega^{2} L^{n}}{n Y}\) where, \(Y\) is Young's modulus of rod, determine value of \(n\).
369790
The graph shows the extension of a wire of length \(1\,m\) suspended from the top of a roof at one end and with a load \({W}\) connected to the other end. If the cross sectional area of the wire is \({1 {~mm}^{2}}\), then the Young's modulus of the material of the wire is
369792 A uniformly tapering conical wire is made from a material of Young's modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values \(R\) and \(3 R\), respectively, The upper end of the wire is fixed to a rigid support and a mass \(M\) is suspended from its lower end. The equilibrium extended length, of this wire, would equal