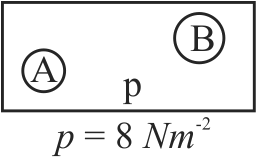361224
Two soap bubbles \(A\) and \(B\) are kept in a closed chamber where the air is maintained at pressure \(8\,N{m^{ - 2}}\). The radii of bubbles \(A\) and \(B\) are \(2\,\;cm\) and \(3\,\;cm\) respectively. Surface tension of the soap-water used to make bubbles is \(0.004\,N{m^{ - 1}}\).
Find the ratio \(\dfrac{n_{B}}{n_{A}}\), where \(n_{A}\) and \(n_{B}\) are the number of moles of air bubbles \(A\) and \(B\), respectively. [Neglect the effect of gravity]
361226 Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible ? The surface tension is \(T\), density of liquid is \(\rho \,{\text{and}}\,L\) is its latent heat of vaporization.
361224
Two soap bubbles \(A\) and \(B\) are kept in a closed chamber where the air is maintained at pressure \(8\,N{m^{ - 2}}\). The radii of bubbles \(A\) and \(B\) are \(2\,\;cm\) and \(3\,\;cm\) respectively. Surface tension of the soap-water used to make bubbles is \(0.004\,N{m^{ - 1}}\).
Find the ratio \(\dfrac{n_{B}}{n_{A}}\), where \(n_{A}\) and \(n_{B}\) are the number of moles of air bubbles \(A\) and \(B\), respectively. [Neglect the effect of gravity]
361226 Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible ? The surface tension is \(T\), density of liquid is \(\rho \,{\text{and}}\,L\) is its latent heat of vaporization.
361224
Two soap bubbles \(A\) and \(B\) are kept in a closed chamber where the air is maintained at pressure \(8\,N{m^{ - 2}}\). The radii of bubbles \(A\) and \(B\) are \(2\,\;cm\) and \(3\,\;cm\) respectively. Surface tension of the soap-water used to make bubbles is \(0.004\,N{m^{ - 1}}\).
Find the ratio \(\dfrac{n_{B}}{n_{A}}\), where \(n_{A}\) and \(n_{B}\) are the number of moles of air bubbles \(A\) and \(B\), respectively. [Neglect the effect of gravity]
361226 Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible ? The surface tension is \(T\), density of liquid is \(\rho \,{\text{and}}\,L\) is its latent heat of vaporization.
361224
Two soap bubbles \(A\) and \(B\) are kept in a closed chamber where the air is maintained at pressure \(8\,N{m^{ - 2}}\). The radii of bubbles \(A\) and \(B\) are \(2\,\;cm\) and \(3\,\;cm\) respectively. Surface tension of the soap-water used to make bubbles is \(0.004\,N{m^{ - 1}}\).
Find the ratio \(\dfrac{n_{B}}{n_{A}}\), where \(n_{A}\) and \(n_{B}\) are the number of moles of air bubbles \(A\) and \(B\), respectively. [Neglect the effect of gravity]
361226 Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible ? The surface tension is \(T\), density of liquid is \(\rho \,{\text{and}}\,L\) is its latent heat of vaporization.
361224
Two soap bubbles \(A\) and \(B\) are kept in a closed chamber where the air is maintained at pressure \(8\,N{m^{ - 2}}\). The radii of bubbles \(A\) and \(B\) are \(2\,\;cm\) and \(3\,\;cm\) respectively. Surface tension of the soap-water used to make bubbles is \(0.004\,N{m^{ - 1}}\).
Find the ratio \(\dfrac{n_{B}}{n_{A}}\), where \(n_{A}\) and \(n_{B}\) are the number of moles of air bubbles \(A\) and \(B\), respectively. [Neglect the effect of gravity]
361226 Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible ? The surface tension is \(T\), density of liquid is \(\rho \,{\text{and}}\,L\) is its latent heat of vaporization.