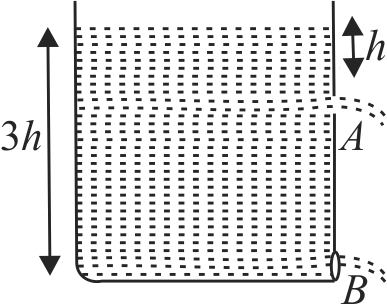
360871 A vessel completely filled with water has holes ' \(A\) ' and ' \(B\) ' at depths ' \(h\) ' and ' \(3 h\) ' from the top, respectively. Hole ' \(A\) ' is a square of side ' \(L\) ' and ' \(B\) ' is circle of radius ' \(r\) '. The water flowing out per second from both the holes is same. Then ' \(L\) ' is equal to
360872
A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve: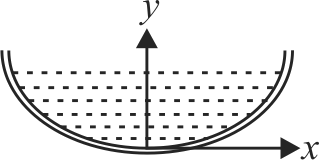
360871 A vessel completely filled with water has holes ' \(A\) ' and ' \(B\) ' at depths ' \(h\) ' and ' \(3 h\) ' from the top, respectively. Hole ' \(A\) ' is a square of side ' \(L\) ' and ' \(B\) ' is circle of radius ' \(r\) '. The water flowing out per second from both the holes is same. Then ' \(L\) ' is equal to
360872
A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve:
360871 A vessel completely filled with water has holes ' \(A\) ' and ' \(B\) ' at depths ' \(h\) ' and ' \(3 h\) ' from the top, respectively. Hole ' \(A\) ' is a square of side ' \(L\) ' and ' \(B\) ' is circle of radius ' \(r\) '. The water flowing out per second from both the holes is same. Then ' \(L\) ' is equal to
360872
A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve:
360871 A vessel completely filled with water has holes ' \(A\) ' and ' \(B\) ' at depths ' \(h\) ' and ' \(3 h\) ' from the top, respectively. Hole ' \(A\) ' is a square of side ' \(L\) ' and ' \(B\) ' is circle of radius ' \(r\) '. The water flowing out per second from both the holes is same. Then ' \(L\) ' is equal to
360872
A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve:
360871 A vessel completely filled with water has holes ' \(A\) ' and ' \(B\) ' at depths ' \(h\) ' and ' \(3 h\) ' from the top, respectively. Hole ' \(A\) ' is a square of side ' \(L\) ' and ' \(B\) ' is circle of radius ' \(r\) '. The water flowing out per second from both the holes is same. Then ' \(L\) ' is equal to
360872
A small hole is made at the bottom of a symmetrical jar as shown in figure. A liquid is filled into the jar upto a certain height. The rate of descension of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve: