360865 A spout pipe of diameter \(0.5\;cm\) is connected horizontally at the bottom of a cylindrical vessel of diameter \(15\;cm\) as shown in figure below.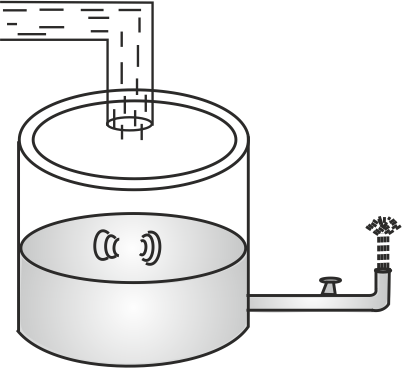


When water is poured into the vessel, it leaves the spout in the form of a fountain. Find the height to which the veritical stream of water goes, if the water level in the vessel is maintained at a constant height of \(0.45\,\,m.\)
(Take \(g = 10\;m{\rm{/}}{s^2}\))

360866 A closed water tank has cross-sectional area \(A\). It has a small hole at a depth of \(h\) from the free surface of water. The radius of the hole is \(r\) so that \(r < < \sqrt{\dfrac{A}{\pi}}\). If \(P_{0}\) is the pressure inside the tank above water level, and \(P_{a}\) is the atmospheric pressure, the rate of flow of the water coming out of the hole is \([\rho\) is the density of water]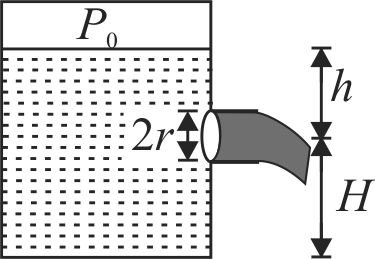

360867 A hole is in the bottom of the tank having water. If total pressure at the bottom is\(3\;{\rm{atm}}\left( {1\;{\rm{atm}} = {{10}^5}\,\,N{m^{ - 2}}} \right)\), then velocity of water flowing from hole is

360868 The level of water in a tank is \(5\;m\) high. A hole of area \(1\;c{m^2}\) is made at the bottom of the tank. The rate of leakage of water from the hole is \(\left( {g = 10\;m/{s^2}} \right)\)

360865 A spout pipe of diameter \(0.5\;cm\) is connected horizontally at the bottom of a cylindrical vessel of diameter \(15\;cm\) as shown in figure below.


When water is poured into the vessel, it leaves the spout in the form of a fountain. Find the height to which the veritical stream of water goes, if the water level in the vessel is maintained at a constant height of \(0.45\,\,m.\)
(Take \(g = 10\;m{\rm{/}}{s^2}\))

360866 A closed water tank has cross-sectional area \(A\). It has a small hole at a depth of \(h\) from the free surface of water. The radius of the hole is \(r\) so that \(r < < \sqrt{\dfrac{A}{\pi}}\). If \(P_{0}\) is the pressure inside the tank above water level, and \(P_{a}\) is the atmospheric pressure, the rate of flow of the water coming out of the hole is \([\rho\) is the density of water]

360867 A hole is in the bottom of the tank having water. If total pressure at the bottom is\(3\;{\rm{atm}}\left( {1\;{\rm{atm}} = {{10}^5}\,\,N{m^{ - 2}}} \right)\), then velocity of water flowing from hole is

360868 The level of water in a tank is \(5\;m\) high. A hole of area \(1\;c{m^2}\) is made at the bottom of the tank. The rate of leakage of water from the hole is \(\left( {g = 10\;m/{s^2}} \right)\)

360865 A spout pipe of diameter \(0.5\;cm\) is connected horizontally at the bottom of a cylindrical vessel of diameter \(15\;cm\) as shown in figure below.


When water is poured into the vessel, it leaves the spout in the form of a fountain. Find the height to which the veritical stream of water goes, if the water level in the vessel is maintained at a constant height of \(0.45\,\,m.\)
(Take \(g = 10\;m{\rm{/}}{s^2}\))

360866 A closed water tank has cross-sectional area \(A\). It has a small hole at a depth of \(h\) from the free surface of water. The radius of the hole is \(r\) so that \(r < < \sqrt{\dfrac{A}{\pi}}\). If \(P_{0}\) is the pressure inside the tank above water level, and \(P_{a}\) is the atmospheric pressure, the rate of flow of the water coming out of the hole is \([\rho\) is the density of water]

360867 A hole is in the bottom of the tank having water. If total pressure at the bottom is\(3\;{\rm{atm}}\left( {1\;{\rm{atm}} = {{10}^5}\,\,N{m^{ - 2}}} \right)\), then velocity of water flowing from hole is

360868 The level of water in a tank is \(5\;m\) high. A hole of area \(1\;c{m^2}\) is made at the bottom of the tank. The rate of leakage of water from the hole is \(\left( {g = 10\;m/{s^2}} \right)\)

360865 A spout pipe of diameter \(0.5\;cm\) is connected horizontally at the bottom of a cylindrical vessel of diameter \(15\;cm\) as shown in figure below.


When water is poured into the vessel, it leaves the spout in the form of a fountain. Find the height to which the veritical stream of water goes, if the water level in the vessel is maintained at a constant height of \(0.45\,\,m.\)
(Take \(g = 10\;m{\rm{/}}{s^2}\))

360866 A closed water tank has cross-sectional area \(A\). It has a small hole at a depth of \(h\) from the free surface of water. The radius of the hole is \(r\) so that \(r < < \sqrt{\dfrac{A}{\pi}}\). If \(P_{0}\) is the pressure inside the tank above water level, and \(P_{a}\) is the atmospheric pressure, the rate of flow of the water coming out of the hole is \([\rho\) is the density of water]

360867 A hole is in the bottom of the tank having water. If total pressure at the bottom is\(3\;{\rm{atm}}\left( {1\;{\rm{atm}} = {{10}^5}\,\,N{m^{ - 2}}} \right)\), then velocity of water flowing from hole is

360868 The level of water in a tank is \(5\;m\) high. A hole of area \(1\;c{m^2}\) is made at the bottom of the tank. The rate of leakage of water from the hole is \(\left( {g = 10\;m/{s^2}} \right)\)