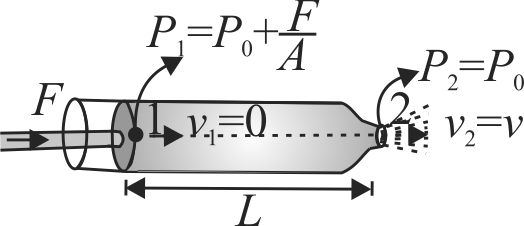
360861 Calculate work should be done (in \(J\) ) in order to squeeze all water from a horizontally located cylinder as shown in figure during the time \(t=10 {~s}\) by means of a container force acting on the piston? The volume of water in the cylinder is equal to \(V=1\) lit, the cross-sectional area of the orifice is \(a=0.5 {~cm}^{2}\), with a being considerably less than the pistol area. The friction and viscosity are negligibly small.

360862 A tank containing liquid has an orifice in one vertical side. If the center of orifice is \(19.6\;m\) below the surface level in the tank. Find the velocity of discharge assuming that is no wastage of energy.

360863 A large tank filled with water to a height ' \(h\) ' is to be emptied through a small hole at the bottom. The ratio of time taken for the level of water to fall from \(h\) to \(\dfrac{h}{2}\) and from \(\dfrac{h}{2}\) to zero is

360864 There is a hole of area \(\frac{1}{{25}}\;c{m^2}\) in the bottom of a cylindrical vessel containing fluid up to height \(h\). The liquid flows out in time \(t\). If the liquid were filled in the vessel up to height \(4 h\), then it would flow out in time

360861 Calculate work should be done (in \(J\) ) in order to squeeze all water from a horizontally located cylinder as shown in figure during the time \(t=10 {~s}\) by means of a container force acting on the piston? The volume of water in the cylinder is equal to \(V=1\) lit, the cross-sectional area of the orifice is \(a=0.5 {~cm}^{2}\), with a being considerably less than the pistol area. The friction and viscosity are negligibly small.

360862 A tank containing liquid has an orifice in one vertical side. If the center of orifice is \(19.6\;m\) below the surface level in the tank. Find the velocity of discharge assuming that is no wastage of energy.

360863 A large tank filled with water to a height ' \(h\) ' is to be emptied through a small hole at the bottom. The ratio of time taken for the level of water to fall from \(h\) to \(\dfrac{h}{2}\) and from \(\dfrac{h}{2}\) to zero is

360864 There is a hole of area \(\frac{1}{{25}}\;c{m^2}\) in the bottom of a cylindrical vessel containing fluid up to height \(h\). The liquid flows out in time \(t\). If the liquid were filled in the vessel up to height \(4 h\), then it would flow out in time

360861 Calculate work should be done (in \(J\) ) in order to squeeze all water from a horizontally located cylinder as shown in figure during the time \(t=10 {~s}\) by means of a container force acting on the piston? The volume of water in the cylinder is equal to \(V=1\) lit, the cross-sectional area of the orifice is \(a=0.5 {~cm}^{2}\), with a being considerably less than the pistol area. The friction and viscosity are negligibly small.

360862 A tank containing liquid has an orifice in one vertical side. If the center of orifice is \(19.6\;m\) below the surface level in the tank. Find the velocity of discharge assuming that is no wastage of energy.

360863 A large tank filled with water to a height ' \(h\) ' is to be emptied through a small hole at the bottom. The ratio of time taken for the level of water to fall from \(h\) to \(\dfrac{h}{2}\) and from \(\dfrac{h}{2}\) to zero is

360864 There is a hole of area \(\frac{1}{{25}}\;c{m^2}\) in the bottom of a cylindrical vessel containing fluid up to height \(h\). The liquid flows out in time \(t\). If the liquid were filled in the vessel up to height \(4 h\), then it would flow out in time

360861 Calculate work should be done (in \(J\) ) in order to squeeze all water from a horizontally located cylinder as shown in figure during the time \(t=10 {~s}\) by means of a container force acting on the piston? The volume of water in the cylinder is equal to \(V=1\) lit, the cross-sectional area of the orifice is \(a=0.5 {~cm}^{2}\), with a being considerably less than the pistol area. The friction and viscosity are negligibly small.

360862 A tank containing liquid has an orifice in one vertical side. If the center of orifice is \(19.6\;m\) below the surface level in the tank. Find the velocity of discharge assuming that is no wastage of energy.

360863 A large tank filled with water to a height ' \(h\) ' is to be emptied through a small hole at the bottom. The ratio of time taken for the level of water to fall from \(h\) to \(\dfrac{h}{2}\) and from \(\dfrac{h}{2}\) to zero is

360864 There is a hole of area \(\frac{1}{{25}}\;c{m^2}\) in the bottom of a cylindrical vessel containing fluid up to height \(h\). The liquid flows out in time \(t\). If the liquid were filled in the vessel up to height \(4 h\), then it would flow out in time