360840
A cylindrical container of radius ' \(R\) ' and height ' \(h\) ' is completely filled with a liqiud. Two horizontal \(L\) shaped pipes of small cross-section area ' \(a\) ' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is:
360841
A horizontal tube of uniform cross-sectional area \(A\) is bent in the form of \(U\)-tube as shown. A liquid of density \(\rho\) enters and leaves the tube with velocity \(v\). External force \(F\) required to hold the tube stationary is
\(F=(x) \times\left(\dfrac{1}{2} \rho a v^{2}\right)\). Find \(x\)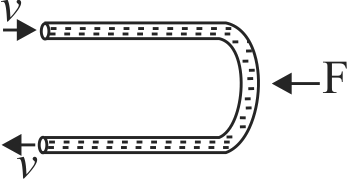
360843
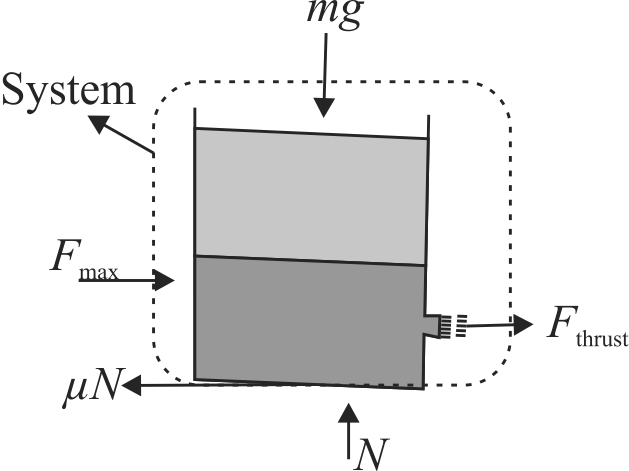
A cylindrical vessel having cross-sectional area \(A=0.5 {~m}^{2}\) is filled with two liquids of density \(\rho_{1}=500 {~kg} {~m}^{-3}\) and \(\rho_{2}=\) \(1000 {~kg} {~m}^{-3}\), to a height \(h=50 {~cm}\) each as shown in figure. A small hole having area \(a=5 {~cm}^{2}\) is made in right vertical wall at a height \(y=10 {~cm}\) from the bottom. Calculate the maximum values of \(F\) to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is \(\mu=0.02\). \(\left(g=10 {~ms}^{-2}\right)\).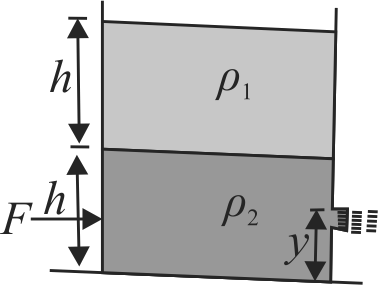
360840
A cylindrical container of radius ' \(R\) ' and height ' \(h\) ' is completely filled with a liqiud. Two horizontal \(L\) shaped pipes of small cross-section area ' \(a\) ' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is:
360841
A horizontal tube of uniform cross-sectional area \(A\) is bent in the form of \(U\)-tube as shown. A liquid of density \(\rho\) enters and leaves the tube with velocity \(v\). External force \(F\) required to hold the tube stationary is
\(F=(x) \times\left(\dfrac{1}{2} \rho a v^{2}\right)\). Find \(x\)
360843
A cylindrical vessel having cross-sectional area \(A=0.5 {~m}^{2}\) is filled with two liquids of density \(\rho_{1}=500 {~kg} {~m}^{-3}\) and \(\rho_{2}=\) \(1000 {~kg} {~m}^{-3}\), to a height \(h=50 {~cm}\) each as shown in figure. A small hole having area \(a=5 {~cm}^{2}\) is made in right vertical wall at a height \(y=10 {~cm}\) from the bottom. Calculate the maximum values of \(F\) to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is \(\mu=0.02\). \(\left(g=10 {~ms}^{-2}\right)\).
360840
A cylindrical container of radius ' \(R\) ' and height ' \(h\) ' is completely filled with a liqiud. Two horizontal \(L\) shaped pipes of small cross-section area ' \(a\) ' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is:
360841
A horizontal tube of uniform cross-sectional area \(A\) is bent in the form of \(U\)-tube as shown. A liquid of density \(\rho\) enters and leaves the tube with velocity \(v\). External force \(F\) required to hold the tube stationary is
\(F=(x) \times\left(\dfrac{1}{2} \rho a v^{2}\right)\). Find \(x\)
360843
A cylindrical vessel having cross-sectional area \(A=0.5 {~m}^{2}\) is filled with two liquids of density \(\rho_{1}=500 {~kg} {~m}^{-3}\) and \(\rho_{2}=\) \(1000 {~kg} {~m}^{-3}\), to a height \(h=50 {~cm}\) each as shown in figure. A small hole having area \(a=5 {~cm}^{2}\) is made in right vertical wall at a height \(y=10 {~cm}\) from the bottom. Calculate the maximum values of \(F\) to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is \(\mu=0.02\). \(\left(g=10 {~ms}^{-2}\right)\).
360840
A cylindrical container of radius ' \(R\) ' and height ' \(h\) ' is completely filled with a liqiud. Two horizontal \(L\) shaped pipes of small cross-section area ' \(a\) ' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is:
360841
A horizontal tube of uniform cross-sectional area \(A\) is bent in the form of \(U\)-tube as shown. A liquid of density \(\rho\) enters and leaves the tube with velocity \(v\). External force \(F\) required to hold the tube stationary is
\(F=(x) \times\left(\dfrac{1}{2} \rho a v^{2}\right)\). Find \(x\)
360843
A cylindrical vessel having cross-sectional area \(A=0.5 {~m}^{2}\) is filled with two liquids of density \(\rho_{1}=500 {~kg} {~m}^{-3}\) and \(\rho_{2}=\) \(1000 {~kg} {~m}^{-3}\), to a height \(h=50 {~cm}\) each as shown in figure. A small hole having area \(a=5 {~cm}^{2}\) is made in right vertical wall at a height \(y=10 {~cm}\) from the bottom. Calculate the maximum values of \(F\) to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is \(\mu=0.02\). \(\left(g=10 {~ms}^{-2}\right)\).
360840
A cylindrical container of radius ' \(R\) ' and height ' \(h\) ' is completely filled with a liqiud. Two horizontal \(L\) shaped pipes of small cross-section area ' \(a\) ' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is:
360841
A horizontal tube of uniform cross-sectional area \(A\) is bent in the form of \(U\)-tube as shown. A liquid of density \(\rho\) enters and leaves the tube with velocity \(v\). External force \(F\) required to hold the tube stationary is
\(F=(x) \times\left(\dfrac{1}{2} \rho a v^{2}\right)\). Find \(x\)
360843
A cylindrical vessel having cross-sectional area \(A=0.5 {~m}^{2}\) is filled with two liquids of density \(\rho_{1}=500 {~kg} {~m}^{-3}\) and \(\rho_{2}=\) \(1000 {~kg} {~m}^{-3}\), to a height \(h=50 {~cm}\) each as shown in figure. A small hole having area \(a=5 {~cm}^{2}\) is made in right vertical wall at a height \(y=10 {~cm}\) from the bottom. Calculate the maximum values of \(F\) to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is \(\mu=0.02\). \(\left(g=10 {~ms}^{-2}\right)\).