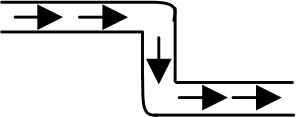
360844 A light cylindrical vessel is kept on a horizontal surface. Its base area is \(A\). A hole of cross sectional area \(a\) is made just at its bottom side. The minimum coefficient of friction necessary for sliding of the vessel due to the the impact force of the emerging liquid is : \((a < < A)\)
360845
There are two identical small holes of area of cross-section \(a\) on the opposite sides of a tank containing a liquid of density \(\rho\). The difference in height between the holes is \(h\). Tank is resting on a smooth horizontal surface. Horizontal force which will have to be applied on the tank to keep it in equilibrium is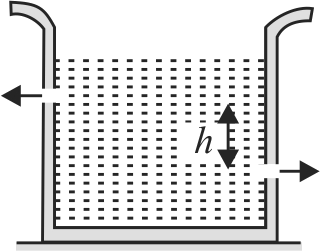
360846
Two streams of water flow through the \(U\)-shaped tubes shown. The tube on the left has cross-sectional area \(A\), and the speed of the water going through it is \(v\); the tube on the right has cross-sectional area \(\dfrac{A}{2}\). If the net force on the tube assembly is zero, what must be the speed \(v^{\prime}\) of the water going through the tube on the right? Neglect gravity, and assume that the speed of the water in each tube is the same upon entry and exit.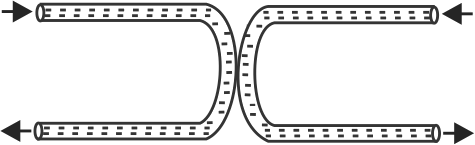
360844 A light cylindrical vessel is kept on a horizontal surface. Its base area is \(A\). A hole of cross sectional area \(a\) is made just at its bottom side. The minimum coefficient of friction necessary for sliding of the vessel due to the the impact force of the emerging liquid is : \((a < < A)\)
360845
There are two identical small holes of area of cross-section \(a\) on the opposite sides of a tank containing a liquid of density \(\rho\). The difference in height between the holes is \(h\). Tank is resting on a smooth horizontal surface. Horizontal force which will have to be applied on the tank to keep it in equilibrium is
360846
Two streams of water flow through the \(U\)-shaped tubes shown. The tube on the left has cross-sectional area \(A\), and the speed of the water going through it is \(v\); the tube on the right has cross-sectional area \(\dfrac{A}{2}\). If the net force on the tube assembly is zero, what must be the speed \(v^{\prime}\) of the water going through the tube on the right? Neglect gravity, and assume that the speed of the water in each tube is the same upon entry and exit.
360844 A light cylindrical vessel is kept on a horizontal surface. Its base area is \(A\). A hole of cross sectional area \(a\) is made just at its bottom side. The minimum coefficient of friction necessary for sliding of the vessel due to the the impact force of the emerging liquid is : \((a < < A)\)
360845
There are two identical small holes of area of cross-section \(a\) on the opposite sides of a tank containing a liquid of density \(\rho\). The difference in height between the holes is \(h\). Tank is resting on a smooth horizontal surface. Horizontal force which will have to be applied on the tank to keep it in equilibrium is
360846
Two streams of water flow through the \(U\)-shaped tubes shown. The tube on the left has cross-sectional area \(A\), and the speed of the water going through it is \(v\); the tube on the right has cross-sectional area \(\dfrac{A}{2}\). If the net force on the tube assembly is zero, what must be the speed \(v^{\prime}\) of the water going through the tube on the right? Neglect gravity, and assume that the speed of the water in each tube is the same upon entry and exit.
360844 A light cylindrical vessel is kept on a horizontal surface. Its base area is \(A\). A hole of cross sectional area \(a\) is made just at its bottom side. The minimum coefficient of friction necessary for sliding of the vessel due to the the impact force of the emerging liquid is : \((a < < A)\)
360845
There are two identical small holes of area of cross-section \(a\) on the opposite sides of a tank containing a liquid of density \(\rho\). The difference in height between the holes is \(h\). Tank is resting on a smooth horizontal surface. Horizontal force which will have to be applied on the tank to keep it in equilibrium is
360846
Two streams of water flow through the \(U\)-shaped tubes shown. The tube on the left has cross-sectional area \(A\), and the speed of the water going through it is \(v\); the tube on the right has cross-sectional area \(\dfrac{A}{2}\). If the net force on the tube assembly is zero, what must be the speed \(v^{\prime}\) of the water going through the tube on the right? Neglect gravity, and assume that the speed of the water in each tube is the same upon entry and exit.