360164
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature \(100 \mathrm{~K}\) and \(200 \mathrm{~K}\) respectively. If the mass of the gas in 1 be \(m\) then what is the mass of the gas in flask 2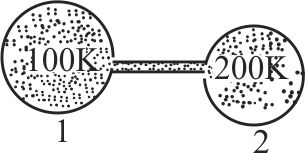
360165
Two diathermic pistons divide an adiabatic container in three equal parts as shown. An ideal gas is present in the three parts \(A,B{\text{ }}\& {\text{ }}C\) having initial pressures as shown and having same temperatures. Now the pistions are released. Then the final equilibrium length of part A after long time will be :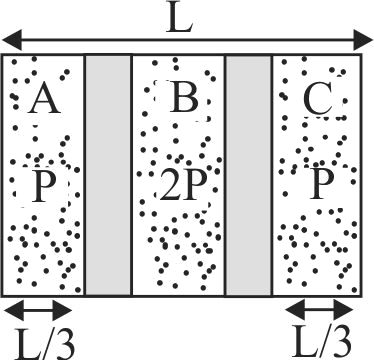
360168 Two thermally insulated vessels 1 and 2 are filled with air at temperatures \(\left(T_{1}, T_{2}\right)\) volume \(\left(V_{1}, V_{2}\right)\) and pressure \(\left(P_{1}, P_{2}\right)\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
360164
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature \(100 \mathrm{~K}\) and \(200 \mathrm{~K}\) respectively. If the mass of the gas in 1 be \(m\) then what is the mass of the gas in flask 2
360165
Two diathermic pistons divide an adiabatic container in three equal parts as shown. An ideal gas is present in the three parts \(A,B{\text{ }}\& {\text{ }}C\) having initial pressures as shown and having same temperatures. Now the pistions are released. Then the final equilibrium length of part A after long time will be :
360168 Two thermally insulated vessels 1 and 2 are filled with air at temperatures \(\left(T_{1}, T_{2}\right)\) volume \(\left(V_{1}, V_{2}\right)\) and pressure \(\left(P_{1}, P_{2}\right)\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
360164
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature \(100 \mathrm{~K}\) and \(200 \mathrm{~K}\) respectively. If the mass of the gas in 1 be \(m\) then what is the mass of the gas in flask 2
360165
Two diathermic pistons divide an adiabatic container in three equal parts as shown. An ideal gas is present in the three parts \(A,B{\text{ }}\& {\text{ }}C\) having initial pressures as shown and having same temperatures. Now the pistions are released. Then the final equilibrium length of part A after long time will be :
360168 Two thermally insulated vessels 1 and 2 are filled with air at temperatures \(\left(T_{1}, T_{2}\right)\) volume \(\left(V_{1}, V_{2}\right)\) and pressure \(\left(P_{1}, P_{2}\right)\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
360164
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature \(100 \mathrm{~K}\) and \(200 \mathrm{~K}\) respectively. If the mass of the gas in 1 be \(m\) then what is the mass of the gas in flask 2
360165
Two diathermic pistons divide an adiabatic container in three equal parts as shown. An ideal gas is present in the three parts \(A,B{\text{ }}\& {\text{ }}C\) having initial pressures as shown and having same temperatures. Now the pistions are released. Then the final equilibrium length of part A after long time will be :
360168 Two thermally insulated vessels 1 and 2 are filled with air at temperatures \(\left(T_{1}, T_{2}\right)\) volume \(\left(V_{1}, V_{2}\right)\) and pressure \(\left(P_{1}, P_{2}\right)\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
360164
Figure shows two flasks connected to each other. The volume of the flask 1 is twice that of flask 2. The system is filled with an ideal gas at temperature \(100 \mathrm{~K}\) and \(200 \mathrm{~K}\) respectively. If the mass of the gas in 1 be \(m\) then what is the mass of the gas in flask 2
360165
Two diathermic pistons divide an adiabatic container in three equal parts as shown. An ideal gas is present in the three parts \(A,B{\text{ }}\& {\text{ }}C\) having initial pressures as shown and having same temperatures. Now the pistions are released. Then the final equilibrium length of part A after long time will be :
360168 Two thermally insulated vessels 1 and 2 are filled with air at temperatures \(\left(T_{1}, T_{2}\right)\) volume \(\left(V_{1}, V_{2}\right)\) and pressure \(\left(P_{1}, P_{2}\right)\) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
