355809
The figure shows all the surfaces are frictionless and mass of the block,\(m = 1\,kg\). The block and wedge are held initially at rest. Now wedge is given a horizontal acceleartion of \(10\,m/{s^2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in \(\sqrt{3}\) seconds is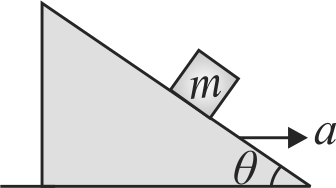
355809
The figure shows all the surfaces are frictionless and mass of the block,\(m = 1\,kg\). The block and wedge are held initially at rest. Now wedge is given a horizontal acceleartion of \(10\,m/{s^2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in \(\sqrt{3}\) seconds is
355809
The figure shows all the surfaces are frictionless and mass of the block,\(m = 1\,kg\). The block and wedge are held initially at rest. Now wedge is given a horizontal acceleartion of \(10\,m/{s^2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in \(\sqrt{3}\) seconds is
355809
The figure shows all the surfaces are frictionless and mass of the block,\(m = 1\,kg\). The block and wedge are held initially at rest. Now wedge is given a horizontal acceleartion of \(10\,m/{s^2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in \(\sqrt{3}\) seconds is
355809
The figure shows all the surfaces are frictionless and mass of the block,\(m = 1\,kg\). The block and wedge are held initially at rest. Now wedge is given a horizontal acceleartion of \(10\,m/{s^2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then work done by the normal force in ground frame on the block in \(\sqrt{3}\) seconds is

