355805
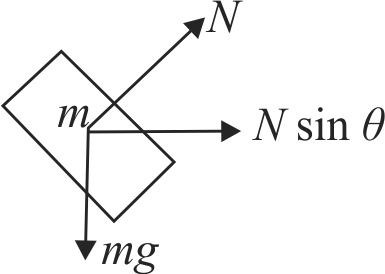
In figure, shown all the surfaces are frictionless, and mass of the block is \(m=100 {~g}\). The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of \(10 {~m} {~s}^{-2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1 \(s\) .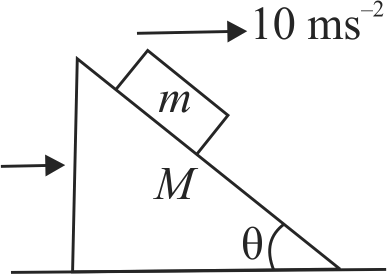
355805
In figure, shown all the surfaces are frictionless, and mass of the block is \(m=100 {~g}\). The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of \(10 {~m} {~s}^{-2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1 \(s\) .
355805
In figure, shown all the surfaces are frictionless, and mass of the block is \(m=100 {~g}\). The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of \(10 {~m} {~s}^{-2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1 \(s\) .
355805
In figure, shown all the surfaces are frictionless, and mass of the block is \(m=100 {~g}\). The block and the wedge are held initially at rest. Now the wedge is given a horizontal acceleration of \(10 {~m} {~s}^{-2}\) by applying a force on the wedge, so that the block does not slip on the wedge. Then find the work done in joules by the normal force in ground frame on the block in 1 \(s\) .