355725
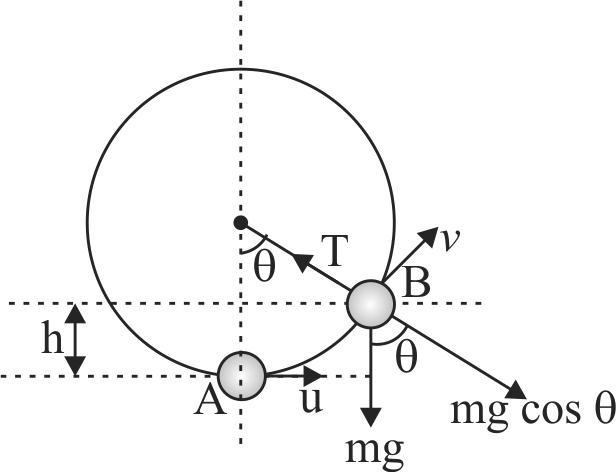
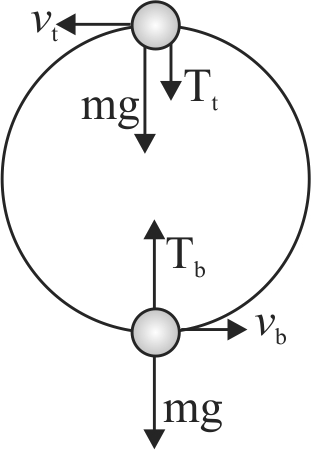
A ball whirls around in a vertical circle at the end of a string. The other end of the string is fixed at the centre of circle. Assuming the total energy of the ball-Earth system remains constant. What is the difference of tension in string at bottom and top during circular motion
\[
\left(T_{\text {bottom }}-T_{\text {top }}=\right.\text { ?) }
\]
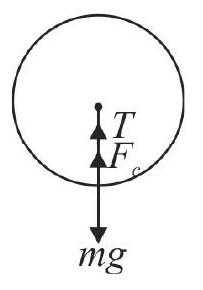
355726 One end of the string of length \(1.0 \mathrm{~m}\) is tied to a body of mass \(0.5 \mathrm{~kg}\). It is whirled in a vertical circle with angular frequency \(4 \mathrm{rad} / \mathrm{s}\). The tension in the string when the body is at the lower most point of its motion will be equal to (take, \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )
355725
A ball whirls around in a vertical circle at the end of a string. The other end of the string is fixed at the centre of circle. Assuming the total energy of the ball-Earth system remains constant. What is the difference of tension in string at bottom and top during circular motion
\[
\left(T_{\text {bottom }}-T_{\text {top }}=\right.\text { ?) }
\]
355726 One end of the string of length \(1.0 \mathrm{~m}\) is tied to a body of mass \(0.5 \mathrm{~kg}\). It is whirled in a vertical circle with angular frequency \(4 \mathrm{rad} / \mathrm{s}\). The tension in the string when the body is at the lower most point of its motion will be equal to (take, \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )
355725
A ball whirls around in a vertical circle at the end of a string. The other end of the string is fixed at the centre of circle. Assuming the total energy of the ball-Earth system remains constant. What is the difference of tension in string at bottom and top during circular motion
\[
\left(T_{\text {bottom }}-T_{\text {top }}=\right.\text { ?) }
\]
355726 One end of the string of length \(1.0 \mathrm{~m}\) is tied to a body of mass \(0.5 \mathrm{~kg}\). It is whirled in a vertical circle with angular frequency \(4 \mathrm{rad} / \mathrm{s}\). The tension in the string when the body is at the lower most point of its motion will be equal to (take, \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )
355725
A ball whirls around in a vertical circle at the end of a string. The other end of the string is fixed at the centre of circle. Assuming the total energy of the ball-Earth system remains constant. What is the difference of tension in string at bottom and top during circular motion
\[
\left(T_{\text {bottom }}-T_{\text {top }}=\right.\text { ?) }
\]
355726 One end of the string of length \(1.0 \mathrm{~m}\) is tied to a body of mass \(0.5 \mathrm{~kg}\). It is whirled in a vertical circle with angular frequency \(4 \mathrm{rad} / \mathrm{s}\). The tension in the string when the body is at the lower most point of its motion will be equal to (take, \(g=10 \mathrm{~m} / \mathrm{s}^{2}\) )